mirror of
https://github.com/Snailclimb/JavaGuide
synced 2025-06-16 18:10:13 +08:00
1037 lines
42 KiB
Markdown
1037 lines
42 KiB
Markdown
---
|
||
title: PriorityQueue 源码分析
|
||
category: Java
|
||
tag:
|
||
- Java集合
|
||
---
|
||
|
||
## PriorityQueue 简介
|
||
|
||
`PriorityQueue` 是 Java 中的一种队列数据结构,被称为 **优先级队列** 。它和普通队列不同,普通队列都是遵循先进先出(FIFO)的原则,即先添加的元素先出队,后添加的元素后出队。而 `PriorityQueue` 则是按照元素的优先级来决定出队的顺序,默认情况下,优先级越小的元素越优先出队。
|
||
|
||

|
||
|
||
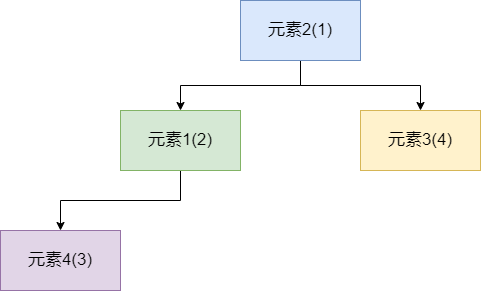
如下图所示,如果是普通队列,我们按照元素 1 到元素 4 的顺序依次入队的话,那么出队的顺序则也是元素 1 到 4。
|
||
|
||

|
||
|
||
而优先队列的逻辑存储结构和普通队列有所不同,以 `PriorityQueue` 为例,其底层实际上是使用 **小顶堆** 形式的二叉堆,即值最小的元素优先出队。
|
||
|
||
可能很多读者对二叉堆的不是很理解,这里笔者以小顶堆为例。假如我们的元素 1 到元素 4 的优先级分别是:2、1、3、4。那么按照 JDK 所提供的小顶堆,元素的排列就会以下面这种形式呈现,可以看到二叉堆这种数据结构符合以下几种性质:
|
||
|
||
1. 二叉堆是一个完全二叉树,即在节点个数无法构成一个满二叉树(每一层节点都排满)时,叶子节点会出现在最后一层,不足双数的情况下叶子节点会尽可能靠左,如下图最后一层只有一个元素 4,就把它放在左边。
|
||
2. 小顶堆的情况下,父节点的值永远小于两个子节点,大顶堆反之。
|
||
3. 二叉堆的大小关系永远只针对父子孙这样的层级,假设我们用的是小顶堆,这并不能说明第二层节点就一定比第三层节点小,如下图的元素 3 和元素 4。
|
||
|
||
|
||
|
||
`PriorityQueue`可以让我们方便地按照优先级执行任务,只要把任务按照优先级放入队列,每次取出的都是优先级最高(值最小)的任务,不用关心排序和出队的细节。
|
||
|
||
简而言之,`PriorityQueue` 适合解决找最大值或最小值的问题,常用于任务调度、事件处理、图论算法等场景。
|
||
|
||
## 手写一个 PriorityQueue
|
||
|
||
JDK 提供的 `PriorityQueue` 用到堆的思想,为了更好地理解 `PriorityQueue` 的底层设计,我会先手写一个二叉堆带读者了解一下二叉堆的基本性质以及 siftUp 和 siftDown 操作。然后,我会基于这个二叉堆模仿 JDK 实现一个自己的 `PriorityQueue` 。
|
||
|
||
并且,最后我还会用自己的 `PriorityQueue` 和 JDK 提供的 `PriorityQueue` 来真正的解决一道经典的 Leetcode 题,帮助大家熟练掌握 `PriorityQueue`。
|
||
|
||
### 二叉堆简介
|
||
|
||
二叉堆从逻辑结构上,我们可以将其看作是一个完全二叉树,而完全二叉树是一种比较特定情况下的树形结构,它有以下几种性质:
|
||
|
||
1. 非叶子节点层次尽可能满。
|
||
2. 叶子节点数量为 `2^(h-1)` 个,注意这里是 h 是从 1 开始算的;如果不满的情况下,叶子节点要尽可能的靠左排列。
|
||
|
||
并且,二叉堆会按照排序的规则分为 **小顶堆** 和 **大顶堆** 。
|
||
|
||
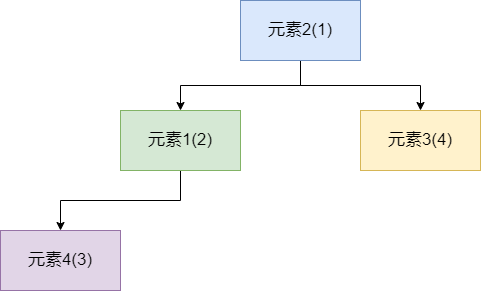
如下图所示,这就是典型的小顶堆,它既像一个完全二叉树(最后一层不满的情况下,节点尽可能靠左,非叶子节点的层节点排满)。又按照小顶堆的规则排列节点,即每一个父节点的值都比它下一层的子节点小。
|
||
|
||
|
||
|
||
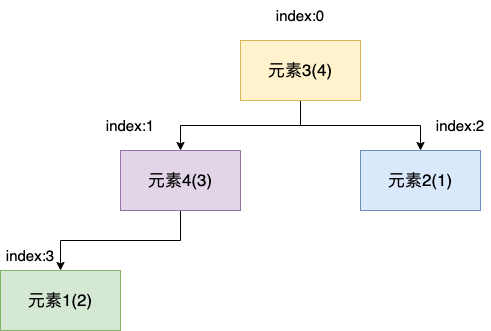
而大顶堆则相反,在符合完全二叉树的性质的情况下,所有的父节点的值都比其下一层的子节点的值大。
|
||
|
||
|
||
|
||
### 基于 JDK 动态数组实现二叉堆
|
||
|
||
为了实现一个二叉堆,我们需要选择合适的数据结构来存储元素。常用的选择有数组和链表,二者在入队和出队操作上的时间复杂度都是 **O(logn)** 。由于链表需要额外的空间来存储节点间的父子关系,而数组可以利用地址连续固定的特点,用简单的公式来表示父子关系。因此,我们选择使用动态数组来实现一个二叉堆,这也是JDK提供的 `PriorityQueue` 的做法。
|
||
|
||
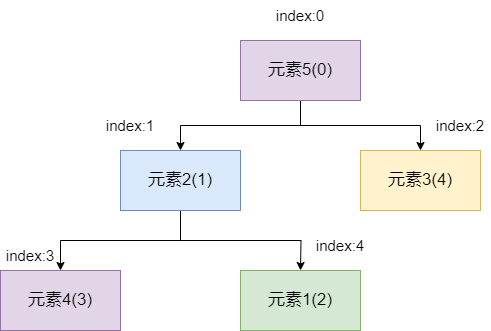
接下来,我们通过观察下图来推导一下这个表示父子关系的公式。
|
||
|
||
|
||
|
||
我们用 `parentIndex` 表示父节点索引,用 `leftIndex` 表示左子节点索引,用 `rightIndex` 表示右子节点。最终,得出以下 3 个公式:
|
||
|
||
1. `leftIndex = 2 * parentIndex+1`
|
||
2. `rightIndex = 2 * parentIndex+2`
|
||
3. `parentIndex=⌊(leftIndex/rightIndex-1)/2⌋`(⌊⌋表示向下取整)
|
||
|
||
得出这套规律之后,我们就可以开始着手编写二叉堆 `MinHeap` 的代码了。
|
||
|
||
#### 源码实现
|
||
|
||
`MinHeap` 类的定义如下:
|
||
|
||
```java
|
||
/**
|
||
* 元素是可比较的小顶堆
|
||
*/
|
||
public class MinHeap<E> {
|
||
|
||
private List<E> list;
|
||
private Comparator<E> comparator;
|
||
// ...
|
||
}
|
||
```
|
||
|
||
只有 2 个比较核心的变量属性,内容如下:
|
||
|
||
- `list`:表示存放元素的列表(底层基于数组)
|
||
- `comparator`:表示比较器对象,如果为空,使用自然排序
|
||
|
||
`MinHeap` 类的构造方法如下,共有 5 个(注释非常清楚,这里就不额外解释了):
|
||
|
||
```java
|
||
/**
|
||
* 创建一个空的最小堆
|
||
*/
|
||
public MinHeap() {
|
||
list = new ArrayList<>();
|
||
}
|
||
|
||
/**
|
||
* 创建一个空的最小堆,并指定比较器来决定元素之间的顺序
|
||
*/
|
||
public MinHeap(Comparator<E> comparator) {
|
||
list = new ArrayList<>();
|
||
this.comparator = comparator;
|
||
}
|
||
|
||
/**
|
||
* 参数为数组,将给定的数组转换为一个最小堆
|
||
*/
|
||
public MinHeap(E[] arr) {
|
||
list = new ArrayList<>(Arrays.asList(arr));
|
||
heapify();
|
||
}
|
||
|
||
/**
|
||
* 创建指定容量的最小堆
|
||
*/
|
||
public MinHeap(int capacity) {
|
||
list = new ArrayList<>(capacity);
|
||
}
|
||
|
||
|
||
/**
|
||
* 创建指定容量的最小堆并指定比较器
|
||
*/
|
||
public MinHeap(int capacity, Comparator<E> comparator) {
|
||
list = new ArrayList<>(capacity);
|
||
this.comparator = comparator;
|
||
}
|
||
```
|
||
|
||
第 3 个构造方法 `MinHeap(E[] arr) ` 涉及到 `heapify()` 方法,我们会再后面进行详细介绍。
|
||
|
||
接下来,我们把集合中一些常见的操作例如获取元素大小、是否为空、获取当前节点左子节点、右子节点、父节点等方法先定义好,比较简单。
|
||
|
||
```java
|
||
/**
|
||
* 返回堆中元素个数
|
||
*/
|
||
public int size() {
|
||
return list.size();
|
||
}
|
||
|
||
/**
|
||
* 判断堆元素是否为空
|
||
*/
|
||
public boolean isEmpty() {
|
||
return list.isEmpty();
|
||
}
|
||
|
||
|
||
/**
|
||
* 获取当前节点的父节点索引
|
||
*/
|
||
private int parentIndex(int childIndex) {
|
||
if (childIndex == 0) {
|
||
throw new IllegalArgumentException();
|
||
}
|
||
|
||
return (childIndex - 1) / 2;
|
||
}
|
||
|
||
/**
|
||
* 返回当前节点的左子节点
|
||
*/
|
||
private int leftIndex(int index) {
|
||
return 2 * index + 1;
|
||
}
|
||
|
||
/**
|
||
* 返回当前节点的右子节点
|
||
*/
|
||
private int rightIndex(int index) {
|
||
return 2 * index + 2;
|
||
}
|
||
```
|
||
|
||
然后,我们再来着手开发一下入队的操作,我们还是以这个小顶堆为例,假如我们现在要插入一个元素 5(优先级为 0),要怎么做呢?
|
||
|
||

|
||
|
||
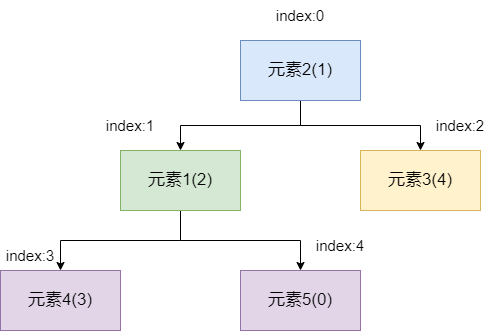
首先我们为了保证元素插入的效率,自然会优先将其添加到数组末端,添加完成之后,我们发现小顶堆失衡了,子节点的值比父节点的值还要小,所以我们需要 `siftUp` 保持一下平衡。
|
||
|
||
|
||
|
||
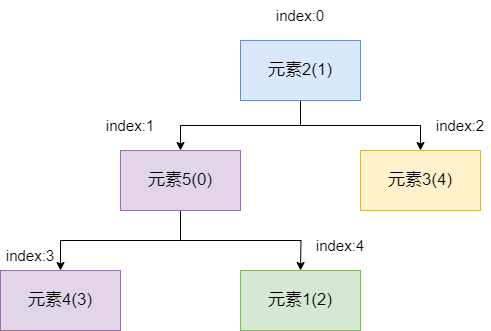
`siftUp` 的操作很简单,首先将元素 5 和其父节点元素 1 比较,发现元素 5 的值比元素 1 的小,两者交换一下位置。
|
||
|
||
|
||
|
||
因为索引 1 位置的元素变为元素 5,所以元素 5 需要再次和当前的父节点比较一下,发现元素 5 的值也比元素 2 的值小,所以两者需要再次交换位置。
|
||
|
||
最终元素 5 到达根节点,无需再进行比较,自此一个新元素入队完成。
|
||
|
||

|
||
|
||
自此我们的编码也可以很快速的编写完成了,代码如下所示,整体步骤为:
|
||
|
||
1. 将新元素插入二叉堆(数组)末端。
|
||
2. 自二叉堆末端开始开始比较,如果当前节点比父节点小,则交换两者的值,直到父节点值比子节点小或者索引为 0 为止。
|
||
|
||
```java
|
||
/**
|
||
* 将元素存到小顶堆中
|
||
*/
|
||
public void add(E e) {
|
||
list.add(e);
|
||
siftUp(list.size() - 1);
|
||
}
|
||
|
||
/**
|
||
* 为了保证新增节点后,数组仍符合小顶堆特性,这里需要siftUp保持一下平衡
|
||
*/
|
||
private void siftUp(int index) {
|
||
if (comparator != null) {
|
||
//循环自新增节点开始自底向上比较子节点和父节点大小,如果子节点大于父节点则交换两者的值
|
||
while (index > 0 && comparator.compare(list.get(parentIndex(index)), list.get(index)) > 0) {
|
||
E tmpElement = list.get(index);
|
||
list.set(index, list.get(parentIndex(index)));
|
||
list.set(parentIndex(index), tmpElement);
|
||
index = parentIndex(index);
|
||
}
|
||
} else {
|
||
//循环自新增节点开始自底向上比较子节点和父节点大小,如果子节点大于父节点则交换两者的值
|
||
while (index > 0 && ((Comparable) list.get(parentIndex(index))).compareTo(list.get(index)) > 0) {
|
||
E tmpElement = list.get(index);
|
||
list.set(index, list.get(parentIndex(index)));
|
||
list.set(parentIndex(index), tmpElement);
|
||
index = parentIndex(index);
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
完成入队操作之后,我们就需要完成出队操作了。
|
||
|
||
还是以上一张图为例,此时我们的小顶堆长这样,出队操作时,我们要将堆顶元素弹出。
|
||
|
||

|
||
|
||
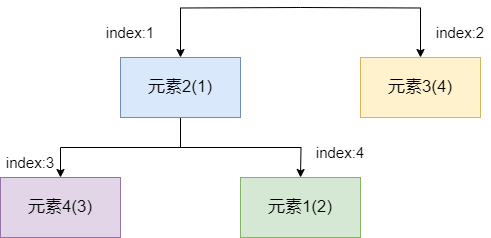
弹出之后,堆顶为空,如果我们单纯的使用左子节点或者右子节点进行 `siftUp`,平均比较次数就会激增,所以最稳妥的做法,是将末端节点移动到堆顶,进行 `siftDown` 操作。
|
||
|
||
|
||
|
||
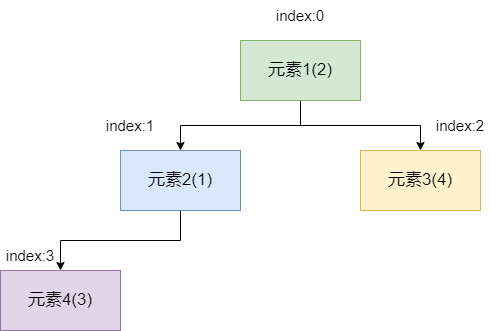
所以我们首先将末端元素移动到堆顶,然后从左右子节点中找到一个最小的和它进行比较,如果存有比它更小的,则交换位置。
|
||
经过比较我们发现元素 2 更小,所以元素 1 要和元素 2 进行位置交换。
|
||
|
||
|
||
|
||
交换完成后如下图所示,此时我们发现元素 1 的值比元素 4 小,所以无需进行交换,比较结束,自此二叉堆的一个出队操作就完成了。
|
||
|
||
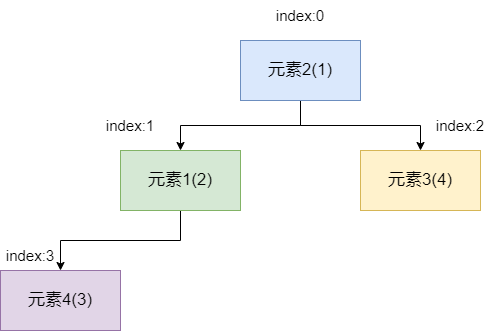
|
||
|
||
所以我们的出队操作的代码也实现了,这里的操作步骤和描述差不多,唯一需要注意的是比较的时候注意判断左右子节点索引计算时必须小于数组大小,避免越界问题。
|
||
|
||
```java
|
||
/**
|
||
* 获取小顶堆堆顶的元素
|
||
*/
|
||
public E poll() {
|
||
if (list == null || list.isEmpty()) {
|
||
return null;
|
||
}
|
||
E ret = list.get(0);
|
||
list.set(0, list.get(list.size() - 1));
|
||
list.remove(list.size() - 1);
|
||
siftDown(0);
|
||
return ret;
|
||
}
|
||
|
||
/**
|
||
* 将数组转为堆
|
||
*/
|
||
private void heapify() {
|
||
//找到最后一个非叶子节点,往前遍历
|
||
for (int i = parentIndex(list.size() - 1); i >= 0; i--) {
|
||
//对每个非叶子节点执行siftDown,使其范围内保持小顶堆特性
|
||
siftDown(i);
|
||
}
|
||
}
|
||
|
||
private void siftDown(int index) {
|
||
|
||
if (comparator != null) {
|
||
//如果左节点小于数组大小才进入循环,避免数组越界
|
||
while (leftIndex(index) < list.size()) {
|
||
//获取左索引
|
||
int cmpIdx = leftIndex(index);
|
||
|
||
//获取左或者右子节点中值更小的索引
|
||
if (rightIndex(index) < list.size() &&
|
||
comparator.compare(list.get(leftIndex(index)), list.get(rightIndex(index))) > 0) {
|
||
cmpIdx = rightIndex(index);
|
||
}
|
||
|
||
//如果父节点比子节点小则停止比较,结束循环
|
||
if (comparator.compare(list.get(index), list.get(cmpIdx)) <= 0) {
|
||
break;
|
||
}
|
||
|
||
//反之交换位置,将index更新为交换后的索引index,进入下一个循环
|
||
E tmpElement = list.get(cmpIdx);
|
||
list.set(cmpIdx, list.get(index));
|
||
list.set(index, tmpElement);
|
||
|
||
|
||
index = cmpIdx;
|
||
|
||
}
|
||
} else {
|
||
//如果左节点小于数组大小才进入循环,避免数组越界
|
||
while (leftIndex(index) < list.size()) {
|
||
//获取左索引
|
||
int cmpIdx = leftIndex(index);
|
||
|
||
//获取左或者右子节点中值更小的索引
|
||
if (rightIndex(index) < list.size() &&
|
||
((Comparable) list.get(leftIndex(index))).compareTo(list.get(rightIndex(index))) > 0) {
|
||
cmpIdx = rightIndex(index);
|
||
}
|
||
|
||
//如果父节点比子节点小则停止比较,结束循环
|
||
if (((Comparable) list.get(index)).compareTo(list.get(cmpIdx)) <= 0) {
|
||
break;
|
||
}
|
||
|
||
//反之交换位置,将index更新为交换后的索引index,进入下一个循环
|
||
E tmpElement = list.get(cmpIdx);
|
||
list.set(cmpIdx, list.get(index));
|
||
list.set(index, tmpElement);
|
||
index = cmpIdx;
|
||
|
||
}
|
||
}
|
||
|
||
|
||
}
|
||
```
|
||
|
||
假如我们现在有下面这样一个数组,我们希望可以将其转换为优先队列,要如何做到呢?你一定觉得,我们遍历数组将元素一个个投入到堆中即可,这样做虽然方便,但是事件复杂度却是 O(n log n),所以笔者现在就要介绍出一种复杂度为 O(n)的方法——`heapify`。
|
||
|
||

|
||
|
||
`heapify` 做法很简单,即从堆的最后一个非叶子节点开始遍历每一个非叶子节点,让这些非叶子节点不断进行 `siftDown` 操作,直到根节点完成 `siftDown` 从而实现快速完成小顶堆的创建。
|
||
|
||
就以上面的数组为例子,如果我们自上而下、自作向右将其看作一个小顶堆,那么它就是下面这张图的样子。
|
||
|
||
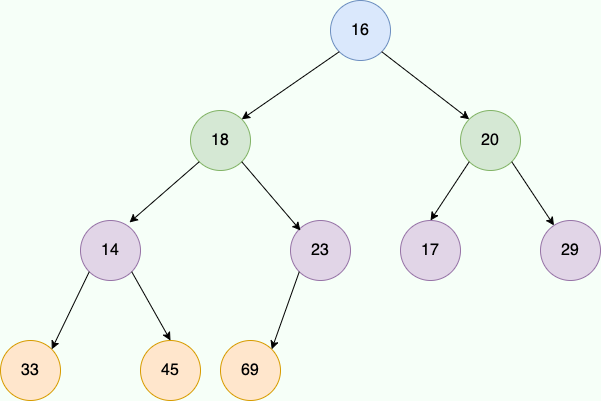
|
||
|
||
首先我们找到最后一个非叶子节点,获取方式很简单,上文说到过二叉堆是一个典型的完全二叉树,假设最后一个叶子节点,即数组的最后一个元素的索引为 `childIndex` 。
|
||
|
||
则我们可以通过下面这个公式得出最后一个非叶子节点:
|
||
|
||
```java
|
||
int parentIndex=(childIndex - 1) / 2
|
||
```
|
||
|
||
是不是很熟悉呢?说白了就是我们上文实现的 `parentIndex` 方法,所以我们定位到了 23,然后 23 这个节点调用 `siftDown` 方法,查看左右节点中有没有比它更小的节点,然后完成交换,在对比过程中发现并没有,于是我们再往前推进,找到到数第二个非叶子节点 14,发现 14 的叶子节点也都比 14 大,所以 `siftDown` 没有进行任何操作,我们再次往前推进。
|
||
|
||
最终我们来到的 20,对 20 进行 `siftDown`,结果发现 17 比 20 小,所以我们将这个两个节点进行交换,交换完成之后 20 到了叶子节点,没有需要进行比较的子节点,本次 `siftDown` 结束。
|
||
|
||
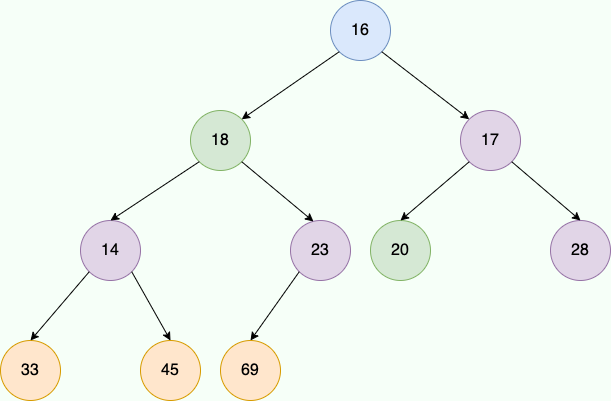
|
||
|
||
继续向前推进,发现 18 的左子节点比 18 小,我们对其进行位置交换,紧接着 18 来到的新位置,发现两个子节点都比 18 大,siftDown 结束。
|
||
|
||
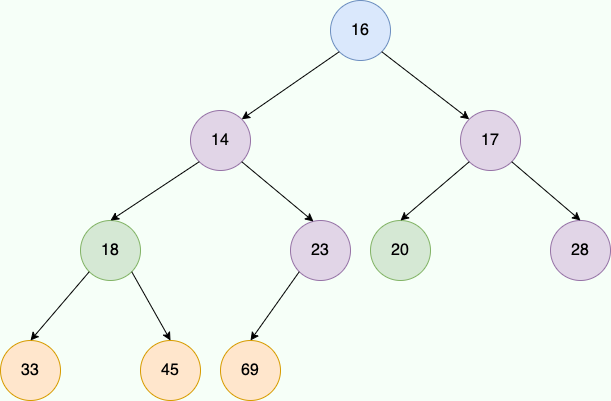
|
||
|
||
最终我们来到了根节点 16,发现左子节点 14 比它小,进行位置交换,然后 16 来到的新位置,发现子节点都比它大,自此数组变为一个标准的小顶堆。
|
||
|
||
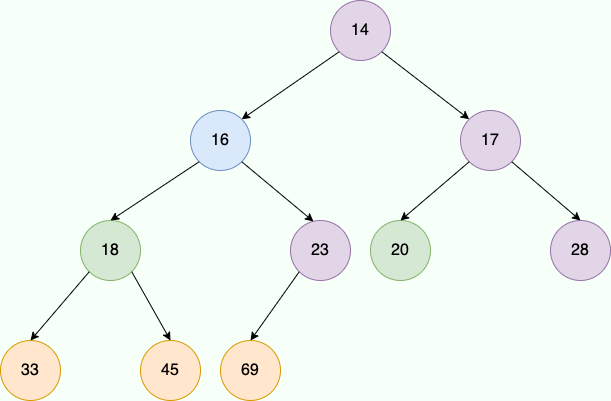
|
||
|
||
了解了整个过程之后,我们的编码工作就变得很简单了,从最后一个非叶子节点往前遍历到根节点,不断执行 `siftDown`,这些都是我们现有的方法所以实现起来就很方便了。
|
||
|
||
```java
|
||
/**
|
||
* 将数组转为堆
|
||
*/
|
||
private void heapify() {
|
||
//找到最后一个非叶子节点,往前遍历
|
||
for (int i = parentIndex(list.size() - 1); i >= 0; i--) {
|
||
//对每个非叶子节点执行siftDown,使其范围内保持小顶堆特性
|
||
siftDown(i);
|
||
}
|
||
}
|
||
```
|
||
|
||
最后,我们再添加一个查看堆顶的元素但不移除的方法 `peek()`。
|
||
|
||
```java
|
||
public E peek() {
|
||
if (list == null || list.isEmpty()) {
|
||
return null;
|
||
}
|
||
return list.get(0);
|
||
}
|
||
```
|
||
|
||
#### 测试
|
||
|
||
为了验证笔者小顶堆各个操作的正确性,笔者编写了下面这样一段测试代码,首先随机生成 1000w 个数据存到小顶堆中,然后进行出队并将元素存到新数组中,进行遍历如果前一个元素比后一个元素大,则说明我们的小顶堆实现的有问题。
|
||
|
||
```java
|
||
int n = 1000_0000;
|
||
|
||
MinHeap<Integer> heap = new MinHeap<>(n, Comparator.comparingInt(a -> a));
|
||
|
||
//往堆中随机存放1000w个元素
|
||
for (int i = 0; i < n; i++) {
|
||
heap.add(ThreadLocalRandom.current().nextInt(0, n));
|
||
}
|
||
|
||
int[] arr = new int[n];
|
||
|
||
//进行出队操作,并将元素存到数组中
|
||
for (int i = 0; i < n; i++) {
|
||
arr[i] = heap.poll();
|
||
}
|
||
|
||
//循环遍历,如果前一个元素比后一个元素大,则说明我们的小顶堆有问题
|
||
for (int i = 1; i < n; i++) {
|
||
if (arr[i - 1] > arr[i]) {
|
||
throw new RuntimeException("err heap");
|
||
}
|
||
}
|
||
```
|
||
|
||
完整源码地址:<https://github.com/Snailclimb/java-code-demo/blob/main/src/main/java/cn/javaguide/datastructures/priorityqueue/MinHeap.java> 。
|
||
|
||
#### 小结
|
||
|
||
自此我们便完成了一个二叉堆的实现,它的入队和出队操作的时间复杂度都是 O(log n),而查询堆顶元素的复杂度则是 O(1);正是这种出色的且均衡的出队效率,使得 JDK 优先队列的实现采用的便是二叉堆的思想,而不是普通数组插入然后按照优先队列进行排序等方案。
|
||
|
||
### 基于二叉堆实现一个 PriorityQueue
|
||
|
||
上文中我们实现了一个小顶堆,此时我们就可以基于这个小顶堆实现一个类似于的 JDK 的优先队列 `PriorityQueue`。
|
||
|
||
在实现优先队列之前,我们需要定义一个队列接口 `Queue<E> `确定一下优先队列所需要具备的行为。
|
||
|
||
```java
|
||
public interface Queue<E> {
|
||
|
||
/**
|
||
* 获取当前队列大小
|
||
*/
|
||
int size();
|
||
|
||
/**
|
||
* 判断当前队列是否为空
|
||
*/
|
||
boolean isEmpty();
|
||
|
||
/**
|
||
* 添加元素到优先队列中
|
||
*/
|
||
boolean offer(E e);
|
||
|
||
/**
|
||
* 返回优先队列优先级最高的元素,如果队列不存在元素则直接返回空
|
||
*/
|
||
E poll();
|
||
|
||
/**
|
||
* 查看优先队列堆顶元素,如果队列为空则返回空
|
||
*/
|
||
E peek();
|
||
}
|
||
```
|
||
|
||
确定了队列应该具备的行为之后,我们就可以基于二叉堆实现优先队列了,由于优先级关系的维护我们已经用二叉堆实现了,所以我们的 `PriorityQueue` 实现也只需对二叉堆进行一个简单的封装即可。
|
||
|
||
```java
|
||
public class PriorityQueue<E extends Comparable> implements Queue<E> {
|
||
|
||
private MinHeap<E> data;
|
||
|
||
|
||
public PriorityQueue() {
|
||
data = new MinHeap<>();
|
||
}
|
||
|
||
public PriorityQueue(Comparator comparator) {
|
||
data = new MinHeap<>(comparator);
|
||
}
|
||
|
||
|
||
@Override
|
||
public int size() {
|
||
return data.size();
|
||
}
|
||
|
||
@Override
|
||
public boolean isEmpty() {
|
||
return data.isEmpty();
|
||
}
|
||
|
||
@Override
|
||
public boolean offer(E e) {
|
||
data.add(e);
|
||
return true;
|
||
}
|
||
|
||
@Override
|
||
public E poll() {
|
||
return data.poll();
|
||
}
|
||
|
||
@Override
|
||
public E peek() {
|
||
return data.peek();
|
||
}
|
||
}
|
||
```
|
||
|
||
我们的测试代码很简单,因为我们优先队列底层采用的是小顶堆,所以我们随机在优先队列中存放 1000w 条数据,然后使用 poll 取出并存到数组中,因为优先队列底层实现用的是小顶堆,所以假如我们的数组前一个元素大于后一个元素,我们即可说明这个优先队列优先级排列有问题,反之则说明我们的优先队列是实现是正确的。
|
||
|
||
```java
|
||
//往队列中随机添加1000_0000条数据
|
||
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
|
||
int n = 1000_0000;
|
||
for (int i = 0; i < n; i++) {
|
||
priorityQueue.offer(ThreadLocalRandom.current().nextInt(1, n));
|
||
}
|
||
|
||
//将优先队列中的数据按照优先级取出并存到数组中
|
||
int[] arr = new int[n];
|
||
|
||
for (int i = 0; i < n; i++) {
|
||
arr[i] = priorityQueue.poll();
|
||
}
|
||
|
||
//如果前一个元素大于后一个元素,则说明优先队列优先级排列有问题
|
||
for (int i = 1; i < arr.length; i++) {
|
||
if (arr[i - 1] > arr[i]) {
|
||
throw new RuntimeException("error PriorityQueue");
|
||
}
|
||
}
|
||
```
|
||
|
||
## JDK 自带 PriorityQueue 使用示例
|
||
|
||
有了手写 `PriorityQueue` 的经验之后,我们对 `PriorityQueue` 已经有了不错的掌握,所以在阅读 `PriorityQueue` 源码前,我们不妨介绍一个 `PriorityQueue` 的使用示例了解一下 JDK 的 `PriorityQueue`。
|
||
|
||
### 基本类型优先队列
|
||
|
||
第一个例子其实和我们手写的测试代码是一样的,可以看出笔者除了添加一个引包逻辑以外,并没有对代码做任何改动,从测试结果来看 JDK 的 PriorityQueue 中的元素也是按照升序进行优先级排列的。
|
||
|
||
```java
|
||
import java.util.PriorityQueue;
|
||
public class Main {
|
||
|
||
|
||
public static void main(String[] args) {
|
||
//往队列中随机添加1000_0000条数据
|
||
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
|
||
int n = 1000_0000;
|
||
for (int i = 0; i < n; i++) {
|
||
priorityQueue.offer(RandomUtil.randomInt(1, n));
|
||
}
|
||
|
||
//将优先队列中的数据按照优先级取出并存到数组中
|
||
int[] arr = new int[n];
|
||
|
||
for (int i = 0; i < n; i++) {
|
||
arr[i] = priorityQueue.poll();
|
||
}
|
||
|
||
//如果前一个元素大于后一个元素,则说明优先队列优先级排列有问题
|
||
for (int i = 1; i < arr.length; i++) {
|
||
if (arr[i - 1] > arr[i]) {
|
||
throw new RuntimeException("error PriorityQueue");
|
||
}
|
||
}
|
||
|
||
}
|
||
}
|
||
```
|
||
|
||
### 特殊类型优先队列
|
||
|
||
假如我们希望将自定义的对象存放到优先队列中,并且我们希望优先级按照年龄进行升序排序,那么我们就可以使用 JDK 的优先队列。
|
||
通过指明队列的泛型以及比较器,我们即可非常方便的实现一个存放自定义对象的优先队列。
|
||
|
||
```java
|
||
public class Example {
|
||
static class Person {
|
||
String name;
|
||
int age;
|
||
|
||
Person(String name, int age) {
|
||
this.name = name;
|
||
this.age = age;
|
||
}
|
||
|
||
public String getName() {
|
||
return name;
|
||
}
|
||
|
||
public int getAge() {
|
||
return age;
|
||
}
|
||
}
|
||
|
||
public static void main(String[] args) {
|
||
PriorityQueue<Person> pq = new PriorityQueue<>(Comparator.comparing(Person::getAge));
|
||
pq.add(new Person("Alice", 25));
|
||
pq.add(new Person("Bob", 30));
|
||
pq.add(new Person("Charlie", 20));
|
||
|
||
while (!pq.isEmpty()) {
|
||
Person p = pq.poll();
|
||
System.out.println(p.getName() + " (" + p.getAge() + ")");
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
## JDK 自带 PriorityQueue 源码分析
|
||
|
||
### 构造函数
|
||
|
||
有了前面手写 `PriorityQueue` 以及 `PriorityQueue` 使用经验之后,我们就可以深入阅读 `PriorityQueue` 源码了。
|
||
|
||
分析源码时,我们可以先看看构造函数了解一下这个类的大概,由于 `PriorityQueue` 构造方法大部分存在复用,所以笔者找到了几个最核心的构造方法。
|
||
|
||
先来看看这个传入数组容量 `initialCapacity` 和比较器的构造方法,可以看到 `PriorityQueue` 的构造方法要求用户传入一个 `initialCapacity` 用于初始化一个数组 `queue`,不难猜出这个数组就是优先队列底层所用到的二叉小顶堆。
|
||
|
||
同时该构造方法还要求用户传入一个 `comparator` 即一个比较器,说明 `queue` 的元素在进行入队操作时是需要比较的,而这个 `comparator` 就是比较的依据。
|
||
|
||
```java
|
||
public PriorityQueue(int initialCapacity,
|
||
Comparator<? super E> comparator) {
|
||
//如果初始化容量小于1则抛出异常
|
||
if (initialCapacity < 1)
|
||
throw new IllegalArgumentException();
|
||
this.queue = new Object[initialCapacity];
|
||
this.comparator = comparator;
|
||
}
|
||
```
|
||
|
||
再来看看另一个核心构造方法,我们发现 PriorityQueue 支持将不同的 Collection 类转为 PriorityQueue,对此我们不妨对每一段逻辑进行深入分析。
|
||
|
||
```java
|
||
public PriorityQueue(Collection<? extends E> c) {
|
||
//SortedSet类型的集合转为PriorityQueue,从SortedSet中获取一个比较器进行初始化,然后按照比较器的规则转移元素到PriorityQueue中
|
||
if (c instanceof SortedSet<?>) {
|
||
SortedSet<? extends E> ss = (SortedSet<? extends E>) c;
|
||
this.comparator = (Comparator<? super E>) ss.comparator();
|
||
initElementsFromCollection(ss);
|
||
}
|
||
//如果集合类型是PriorityQueue则获取PriorityQueue的比较器,并将PriorityQueue的元素转移到我们的PriorityQueue中
|
||
else if (c instanceof PriorityQueue<?>) {
|
||
PriorityQueue<? extends E> pq = (PriorityQueue<? extends E>) c;
|
||
this.comparator = (Comparator<? super E>) pq.comparator();
|
||
initFromPriorityQueue(pq);
|
||
}
|
||
else {
|
||
this.comparator = null;
|
||
initFromCollection(c);
|
||
}
|
||
}
|
||
```
|
||
|
||
当集合类型为 `SortedSet` 时,因为 `SortedSet` 是天生有序的,所以 `PriorityQueue` 直接获取其比较器之后,调用了一个 `initElementsFromCollection`,我们不妨看看 `initElementsFromCollection` 具体做了些什么。
|
||
|
||
```java
|
||
//SortedSet类型的集合转为PriorityQueue,从SortedSet中获取一个比较器进行初始化,然后按照比较器的规则转移元素到PriorityQueue中
|
||
if (c instanceof SortedSet<?>) {
|
||
SortedSet<? extends E> ss = (SortedSet<? extends E>) c;
|
||
this.comparator = (Comparator<? super E>) ss.comparator();
|
||
initElementsFromCollection(ss);
|
||
}
|
||
```
|
||
|
||
可以看到 `initElementsFromCollection` 只不过是将集合元素转为数组,然后赋值给优先队列底层的数组成员变量 queue。`当` a 数组未能返回一个 `Object[]`类型时,则调用 `Arrays.copyOf` 方法将其转为为一个正确的 `Object[]`数组。
|
||
然后遍历元素进行判空,一切正常则将其赋值给 `queue`,并记录此时 `queue` 的长度。
|
||
|
||
```java
|
||
private void initElementsFromCollection(Collection<? extends E> c) {
|
||
Object[] a = c.toArray();
|
||
// If c.toArray incorrectly doesn't return Object[], copy it.
|
||
if (a.getClass() != Object[].class)
|
||
a = Arrays.copyOf(a, a.length, Object[].class);
|
||
int len = a.length;
|
||
if (len == 1 || this.comparator != null)
|
||
for (int i = 0; i < len; i++)
|
||
if (a[i] == null)
|
||
throw new NullPointerException();
|
||
this.queue = a;
|
||
this.size = a.length;
|
||
}
|
||
```
|
||
|
||
我们再来看看 `PriorityQueue` 集合传入时的处理逻辑,同样的将 `PriorityQueue` 的比较器赋值给当前 `PriorityQueue` 之后,调用了一个 `initFromPriorityQueue` 方法,我们步入看看。
|
||
|
||
```java
|
||
//如果集合类型是PriorityQueue则获取PriorityQueue的比较器,并将PriorityQueue的元素转移到我们的PriorityQueue中
|
||
else if (c instanceof PriorityQueue<?>) {
|
||
PriorityQueue<? extends E> pq = (PriorityQueue<? extends E>) c;
|
||
this.comparator = (Comparator<? super E>) pq.comparator();
|
||
initFromPriorityQueue(pq);
|
||
}
|
||
```
|
||
|
||
可以看到 `initFromPriorityQueue` 操作就是让传入的 `PriorityQueue` 通过 `toArray` 返回底层的小顶堆数组,然后赋值给我们的 `PriorityQueue`,在记录一下当前 `PriorityQueue` 的长度。
|
||
|
||
```java
|
||
private void initFromPriorityQueue(PriorityQueue<? extends E> c) {
|
||
if (c.getClass() == PriorityQueue.class) {
|
||
this.queue = c.toArray();
|
||
this.size = c.size();
|
||
} else {
|
||
//略
|
||
}
|
||
}
|
||
```
|
||
|
||
对于一般集合,我们的逻辑会走到这里,默认设置比较器为空,然后也调用了 `initFromCollection`,我们步入查看逻辑。
|
||
|
||
```java
|
||
else {
|
||
this.comparator = null;
|
||
initFromCollection(c);
|
||
}
|
||
```
|
||
|
||
对于非 `PriorityQueue` 的集合,它调用了 `initFromCollection`,我们步入看看。
|
||
|
||
```java
|
||
private void initFromPriorityQueue(PriorityQueue<? extends E> c) {
|
||
if (c.getClass() == PriorityQueue.class) {
|
||
//略
|
||
} else {
|
||
initFromCollection(c);
|
||
}
|
||
}
|
||
```
|
||
|
||
可以看到它的实现就是调用上文所介绍的 `initElementsFromCollection` 将数组存到 `queue` 中,然后调用一个 `heapify` 将这个数组转为小顶堆。
|
||
|
||
```java
|
||
private void initFromCollection(Collection<? extends E> c) {
|
||
initElementsFromCollection(c);
|
||
heapify();
|
||
}
|
||
```
|
||
|
||
对于 JDK 实现的 `heapify`,可以发现它的逻辑和我们所实现的差不多,只不过获取父节点的操作使用了高效的右移运算,同样的遍历所有非叶子节点进行 `siftDown` 生成一个完整的小顶堆。
|
||
|
||
```java
|
||
private void heapify() {
|
||
for (int i = (size >>> 1) - 1; i >= 0; i--)
|
||
siftDown(i, (E) queue[i]);
|
||
}
|
||
```
|
||
|
||
### 入队操作
|
||
|
||
对于 PriorityQueue 来说,核心的入队就是 offer,它的核心步骤为:
|
||
|
||
1. 校验元素是否为空。
|
||
2. 设置新插入的位置为 size。
|
||
3. 判断数组容量是否足够,如果不够则扩容。
|
||
4. 如果是第一个元素,则直接将其放到索引 0 位置。
|
||
5. 如果不是第一个元素,则调用 `siftUp` 将元素放入队列。
|
||
|
||
```java
|
||
public boolean offer(E e) {
|
||
//校验元素是否为空
|
||
if (e == null)
|
||
throw new NullPointerException();
|
||
modCount++;
|
||
//设置新插入的位置为size
|
||
int i = size;
|
||
//判断数组容量是否足够,如果不够则扩容
|
||
if (i >= queue.length)
|
||
grow(i + 1);
|
||
size = i + 1;
|
||
//如果是第一个元素,则直接将其放到索引0位置
|
||
if (i == 0)
|
||
queue[0] = e;
|
||
else
|
||
//如果不是第一个元素,则调用siftUp将元素放入队列
|
||
siftUp(i, e);
|
||
return true;
|
||
}
|
||
```
|
||
|
||
在 `siftUp` 操作时会判断比较器是否为空,如果不为空则使用传入的比较器生成小顶堆,反之就将元素 x 转为 `Comparable` 对象进行比较。
|
||
因为整体比较逻辑都一样,所以我们就以 `siftUpUsingComparator` 查看一下进行 `siftUp` 操作时对于入队元素的处理逻辑。
|
||
|
||
```java
|
||
private void siftUp(int k, E x) {
|
||
if (comparator != null)
|
||
siftUpUsingComparator(k, x);
|
||
else
|
||
siftUpComparable(k, x);
|
||
}
|
||
```
|
||
|
||
`siftUpUsingComparator` 和我们手写的 `siftUp` 逻辑差不多,都是不断向上比较父节点,找到比自己大的则交换位置,直到到达根节点或者比较父节点比自己小为止,整体来说 `PriorityQueue` 的 `siftUp` 分为以下几个步骤:
|
||
|
||
1. 获取入队元素当前索引位置的父索引 parent。
|
||
2. 根据父索引找到元素 e。
|
||
3. 如果新节点 x 比 e 大,则说明当前入队操作符合小顶堆要求,直接结束循环。
|
||
4. 如果 x 比 e 小,则将父节点 e 的值改为我们入队元素 x 的值。
|
||
5. k 指向父索引,继续循环向上比较父索引,直到找到比 x 还小的父节点 e,终止循环。
|
||
6. 将 x 存到符合要求的索引位置 k。
|
||
|
||
```java
|
||
private void siftUpUsingComparator(int k, E x) {
|
||
while (k > 0) {
|
||
//获取入队元素当前索引位置的父索引parent
|
||
int parent = (k - 1) >>> 1;
|
||
//根据父索引找到元素e
|
||
Object e = queue[parent];
|
||
// 如果新节点x比e大,则说明当前入队操作符合小顶堆要求,直接结束循环
|
||
if (comparator.compare(x, (E) e) >= 0)
|
||
break;
|
||
//如果x比e小,则将父节点e的值改为我们入队元素x的值
|
||
queue[k] = e;
|
||
//k指向父索引,继续循环向上比较父索引,直到找到比x还小的父节点e,终止循环
|
||
k = parent;
|
||
}
|
||
//将x存到符合要求的索引位置k
|
||
queue[k] = x;
|
||
}
|
||
```
|
||
|
||
### 出队操作
|
||
|
||
出队操作和我们手写的逻辑也差不多,只不过逻辑处理的更加细致,它的逻辑步骤为:
|
||
|
||
1. size 减 1 并赋值给 s。
|
||
2. 如果队列为空则返回 null。
|
||
3. 如果队列不为空则拷贝索引 0 位置即优先级最高的元素。
|
||
4. 将数组 0 位置设置为 null。
|
||
5. 如果 s 不为 0,说明队列中不止一个元素,需要维持小顶堆的特性,需要从堆顶开始进行 siftDown 操作。
|
||
6. 返回优先队列优先级最高的元素 result。
|
||
|
||
```java
|
||
public E poll() {
|
||
if (size == 0)
|
||
return null;
|
||
int s = --size;
|
||
modCount++;
|
||
E result = (E) queue[0];
|
||
E x = (E) queue[s];
|
||
queue[s] = null;
|
||
if (s != 0)
|
||
siftDown(0, x);
|
||
return result;
|
||
}
|
||
```
|
||
|
||
### 查看优先级最高的元素
|
||
|
||
peek 方法可以不改变队列结构查看优先级最高的元素,如果队列为空则返回 null,反之返回 0 索引位置的元素。
|
||
|
||
```java
|
||
public E peek() {
|
||
return (size == 0) ? null : (E) queue[0];
|
||
}
|
||
```
|
||
|
||
## Leetcode 中关于 PriorityQueue 的使用
|
||
|
||
### 问题
|
||
|
||
因为优先队列自带优先级排列的天然优势,所以使用优先队列进行一些词频统计等操作也是非常快速和方便的。
|
||
|
||
就比如 [Leetcode 347. 前 K 个高频元素](https://leetcode.cn/problems/top-k-frequent-elements/) 这道题目,它要求我们返回整数数组中前 k 个高频元素,常规做法我们可以会将元素存放到 `map` 中,然后对这个 `map` 进行排序,尽管它确实可以完成这个题目,但是从排序和复杂度和优先队列差不多都是 `O(n log n)`,但在实现的复杂度上,在 `PriorityQueue` 的封装下,使用 `PriorityQueue` 来存放元素以及从元素中获取前 k 个元素的操作,相比于前者,同样的思想下后者的实现会更简单一些。
|
||
|
||

|
||
|
||
### 实现思路
|
||
|
||
解决这个问题我们需要统计一下词频,所以我们需要借助额外的集合,所以整体步骤为:
|
||
|
||
1. 用一个 map 记录一下每一个元素的频率。
|
||
2. 创建一个优先队列,比较这个 map 中的 value,按照 value 生成优先队列。
|
||
3. 如果队列长度小于 k(即题目要求返回的前 k 个高频元素),则直接将元素存入队列。
|
||
4. 如果队列长度等于 k,则比较优先队列中队首的元素(value 最小的元素)是否比要入队的元素,如果入队元素比队首元素大,则说明入队元素出现频率比队首元素更频繁,则移除队首元素,再将新添加的元素入队。
|
||
5. 遍历优先队列元素,存放到数组中返回。
|
||
|
||
最终我们就实现了这套完整的代码:
|
||
|
||
```java
|
||
public int[] topKFrequent(int[] nums, int k) {
|
||
//统计各个元素出现的频率并存到map中
|
||
HashMap<Integer, Integer> map = new HashMap<>();
|
||
for (int num : nums) {
|
||
if (!map.containsKey(num)) {
|
||
map.put(num, 1);
|
||
} else {
|
||
map.put(num, map.get(num) + 1);
|
||
}
|
||
}
|
||
|
||
//优先队列按照map的value进行升序排序
|
||
PriorityQueue<Integer> queue = new PriorityQueue<>(Comparator.comparingInt(map::get));
|
||
|
||
//遍历map,筛选出前k个高频元素
|
||
map.entrySet().forEach(e -> {
|
||
if (queue.size() < k) {
|
||
queue.add(e.getKey());
|
||
} else if (e.getValue() > map.get(queue.peek())) {
|
||
queue.remove();
|
||
queue.add(e.getKey());
|
||
}
|
||
});
|
||
|
||
//转为数组返回
|
||
int[] arr = queue.stream().mapToInt(Integer::intValue).toArray();
|
||
return arr;
|
||
|
||
}
|
||
```
|
||
|
||
可以看到代码放到 Leetcode 上执行通过了。
|
||
|
||

|
||
|
||
同样的,笔者也尝试过用自己的手写的优先队列解决这个问题,实现步骤几乎是一致的。
|
||
|
||
```java
|
||
public int[] topKFrequent(int[] nums, int k) {
|
||
HashMap<Integer, Integer> map = new HashMap<>();
|
||
for (int num : nums) {
|
||
if (!map.containsKey(num)) {
|
||
map.put(num, 1);
|
||
} else {
|
||
map.put(num, map.get(num) + 1);
|
||
}
|
||
}
|
||
|
||
|
||
PriorityQueue<Integer> queue = new PriorityQueue<>(Comparator.comparingInt(map::get));
|
||
|
||
map.entrySet().forEach(e -> {
|
||
if (queue.size() < k) {
|
||
queue.offer(e.getKey());
|
||
} else if (e.getValue() > map.get(queue.peek())) {
|
||
queue.poll();
|
||
queue.offer(e.getKey());
|
||
}
|
||
});
|
||
|
||
|
||
List<Integer> list = new ArrayList<>();
|
||
while (!queue.isEmpty()) {
|
||
list.add(queue.poll());
|
||
}
|
||
|
||
return list.stream().mapToInt(Integer::intValue).toArray();
|
||
|
||
}
|
||
|
||
public static void main(String[] args) {
|
||
int[] nums = {1,1,32,312,3,432,412412412,44,4,444,444,4,4,4,4,4,4,4,4,4,6,6,6,6,6,4,4,4,44,3,4324,34,23432,4324,324,324,324,3242,34};
|
||
int k = 2;
|
||
for (int i : (new Solution()).topKFrequent(nums, k)) {
|
||
System.out.println(i);
|
||
}
|
||
}
|
||
```
|
||
|
||
## PriorityQueue 常见面试题
|
||
|
||
### PriorityQueue 为什么要用二叉堆实现,二叉堆有什么使用优势吗?
|
||
|
||
这个问题我们可以用反证法来分析:
|
||
|
||
1. 假如我们使用排序的数组,那么入队操作则是 O(1),但出队操作确实得我们需要遍历一遍数组找到最小的哪一个,所以复杂度为 O(n)。
|
||
2. 假如我们使用有序数组来实现,那么入队操作则因为需要排序变为 O(n),而出队操作则变为 O(1)。
|
||
所以折中考虑,使用带有完全二叉树性质的二叉堆,使得入队和出队操作都是 O(log^n)最合适。
|
||
|
||
### PriorityQueue 是线程安全的吗?
|
||
|
||
我们随意查看入队源码,没有任何针对线程安全的处理操作,所以它是非线程安全的。
|
||
|
||
### PriorityQueue 底层是用什么实现的?初始化容量是多少?
|
||
|
||
我们查看 `PriorityQueue` 的默认构造方法,可以看到 `PriorityQueue` 底层使用一个数组来表示优先队列,而这个数组实际上用到的 **小顶堆** 的思想来维持优先级的。
|
||
|
||
初始化容量我们可以查看构造方法有一个`DEFAULT_INITIAL_CAPACITY,DEFAULT_INITIAL_CAPACITY` 用于初始化数组,查看其定义可以发现默认初始化容量大小为 11。
|
||
|
||
```java
|
||
private static final int DEFAULT_INITIAL_CAPACITY = 11;
|
||
public PriorityQueue() {
|
||
this(DEFAULT_INITIAL_CAPACITY, null);
|
||
}
|
||
```
|
||
|
||
### 如果我希望 PriorityQueue 按照从大到小的顺序排序要怎么做?
|
||
|
||
因为 `PriorityQueue` 底层的数组实现的是一个小顶堆,所以如果我们希望按照降序排列可以将比较器取反一下即可。
|
||
|
||
示例代码:
|
||
|
||
```java
|
||
public static void main(String[] args) {
|
||
//将比较器取反一下实现升序排列
|
||
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(Comparator.comparingInt(Integer::intValue).reversed());
|
||
//随机插入10个元素
|
||
int n = 10;
|
||
for (int i = 0; i < n; i++) {
|
||
int num = RandomUtil.randomInt(1, n);
|
||
System.out.println("add " + num);
|
||
priorityQueue.offer(num);
|
||
}
|
||
|
||
//输出看看是否符合预期
|
||
int s = priorityQueue.size();
|
||
for (int i = 0; i < s; i++) {
|
||
System.out.println(priorityQueue.poll());
|
||
}
|
||
|
||
}
|
||
```
|
||
|
||
### 为什么 PriorityQueue 底层用数组构成小顶堆而不是使用链表呢?
|
||
|
||
先说结论: **使用数组避免了为维护父子及左邻右舍等节点关系的内存空间占用** 。
|
||
|
||
**为什么还要维护左邻右舍关系呢?** 我们都知道 `PriorityQueue` 支持传入一个集合生成优先队列,假如我们传入的是一个无序的 `List`,那么在数组转二叉堆时需要经过一个 `heapify` 的操作,该操作需要从最后一个非叶子节点开始,直到根节点为止,不断 `siftDown` 维持自己以及子孙节点间的优先级关系。
|
||
|
||
如果使用链表这些关系的维护就变得繁琐且占用内存空间,使用数组就不一样了,因为地址的连续性和明确性,我们定位邻节点只需按照公式获得最后一个非叶子节点的索引,然后不断减一就能到达邻节点了。
|
||
|
||
综上所述,使用数组可以以`O(1)` 的时间复杂度定位到最后一个非叶子节点,通过一个减 1 操作即到达下一个非叶子节点,这种轻量级的关系维护是链表所不具备的。
|
||
|
||
## 参考
|
||
|
||
- 面试题:PriorityQueue 底层是什么,初始容量是多少,扩容方式呢:<https://www.cnblogs.com/dalianpai/p/14282030.html>
|
||
- Java Comparator comparingInt() 的使用:<https://blog.csdn.net/qq_46092061/article/details/116402145>
|
||
- 玩儿转数据结构 : <https://github.com/liuyubobobo/Play-with-Data-Structures> |