mirror of
https://github.com/Snailclimb/JavaGuide
synced 2025-06-16 18:10:13 +08:00
774 lines
32 KiB
Markdown
774 lines
32 KiB
Markdown
---
|
||
title: Redis为什么用跳表实现有序集合
|
||
category: 数据库
|
||
tag:
|
||
- Redis
|
||
---
|
||
|
||
## 前言
|
||
|
||
近几年针对 Redis 面试时会涉及常见数据结构的底层设计,其中就有这么一道比较有意思的面试题:“Redis 的有序集合底层为什么要用跳表,而不用平衡树、红黑树或者 B+树?”。
|
||
|
||
本文就以这道大厂常问的面试题为切入点,带大家详细了解一下跳表这个数据结构。
|
||
|
||
本文整体脉络如下图所示,笔者会从有序集合的基本使用到跳表的源码分析和实现,让你会对 Redis 的有序集合底层实现的跳表有着更深刻的理解和掌握。
|
||
|
||
|
||
|
||
## 跳表在 Redis 中的运用
|
||
|
||
这里我们需要先了解一下 Redis 用到跳表的数据结构有序集合的使用,Redis 有个比较常用的数据结构叫**有序集合(sorted set,简称 zset)**,正如其名它是一个可以保证有序且元素唯一的集合,所以它经常用于排行榜等需要进行统计排列的场景。
|
||
|
||
这里我们通过命令行的形式演示一下排行榜的实现,可以看到笔者分别输入 3 名用户:**xiaoming**、**xiaohong**、**xiaowang**,它们的 **score** 分别是 60、80、60,最终按照成绩升级降序排列。
|
||
|
||
```bash
|
||
|
||
127.0.0.1:6379> zadd rankList 60 xiaoming
|
||
(integer) 1
|
||
127.0.0.1:6379> zadd rankList 80 xiaohong
|
||
(integer) 1
|
||
127.0.0.1:6379> zadd rankList 60 xiaowang
|
||
(integer) 1
|
||
|
||
# 返回有序集中指定区间内的成员,通过索引,分数从高到低
|
||
127.0.0.1:6379> ZREVRANGE rankList 0 100 WITHSCORES
|
||
1) "xiaohong"
|
||
2) "80"
|
||
3) "xiaowang"
|
||
4) "60"
|
||
5) "xiaoming"
|
||
6) "60"
|
||
```
|
||
|
||
此时我们通过 `object` 指令查看 zset 的数据结构,可以看到当前有序集合存储的还是 **ziplist(压缩列表)**。
|
||
|
||
```bash
|
||
127.0.0.1:6379> object encoding rankList
|
||
"ziplist"
|
||
```
|
||
|
||
因为设计者考虑到 Redis 数据存放于内存,为了节约宝贵的内存空间,在有序集合元素小于 64 字节且个数小于 128 的时候,会使用 ziplist,而这个阈值的默认值的设置就来自下面这两个配置项。
|
||
|
||
```bash
|
||
zset-max-ziplist-value 64
|
||
zset-max-ziplist-entries 128
|
||
```
|
||
|
||
一旦有序集合中的某个元素超出这两个其中的一个阈值,它就会转为 **skiplist**(实际是 dict+skiplist,还会借用字典来提高获取指定元素的效率)。
|
||
|
||
我们不妨在添加一个大于 64 字节的元素,可以看到有序集合的底层存储转为 skiplist。
|
||
|
||
```bash
|
||
127.0.0.1:6379> zadd rankList 90 yigemingzihuichaoguo64zijiedeyonghumingchengyongyuceshitiaobiaodeshijiyunyong
|
||
(integer) 1
|
||
|
||
# 超过阈值,转为跳表
|
||
127.0.0.1:6379> object encoding rankList
|
||
"skiplist"
|
||
```
|
||
|
||
也就是说,ZSet 有两种不同的实现,分别是 ziplist 和 skiplist,具体使用哪种结构进行存储的规则如下:
|
||
|
||
- 当有序集合对象同时满足以下两个条件时,使用 ziplist:
|
||
1. ZSet 保存的键值对数量少于 128 个;
|
||
2. 每个元素的长度小于 64 字节。
|
||
- 如果不满足上述两个条件,那么使用 skiplist。
|
||
|
||
## 手写一个跳表
|
||
|
||
为了更好的回答上述问题以及更好的理解和掌握跳表,这里可以通过手写一个简单的跳表的形式来帮助读者理解跳表这个数据结构。
|
||
|
||
我们都知道有序链表在添加、查询、删除的平均时间复杂都都是 **O(n)** 即线性增长,所以一旦节点数量达到一定体量后其性能表现就会非常差劲。而跳表我们完全可以理解为在原始链表基础上,建立多级索引,通过多级索引检索定位将增删改查的时间复杂度变为 **O(log n)**。
|
||
|
||
可能这里说的有些抽象,我们举个例子,以下图跳表为例,其原始链表存储按序存储 1-10,有 2 级索引,每级索引的索引个数都是基于下层元素个数的一半。
|
||
|
||

|
||
|
||
假如我们需要查询元素 6,其工作流程如下:
|
||
|
||
1. 从 2 级索引开始,先来到节点 4。
|
||
2. 查看 4 的后继节点,是 8 的 2 级索引,这个值大于 6,说明 2 级索引后续的索引都是大于 6 的,没有再往后搜寻的必要,我们索引向下查找。
|
||
3. 来到 4 的 1 级索引,比对其后继节点为 6,查找结束。
|
||
|
||
相较于原始有序链表需要 6 次,我们的跳表通过建立多级索引,我们只需两次就直接定位到了目标元素,其查寻的复杂度被直接优化为 **O(log n)**。
|
||
|
||

|
||
|
||
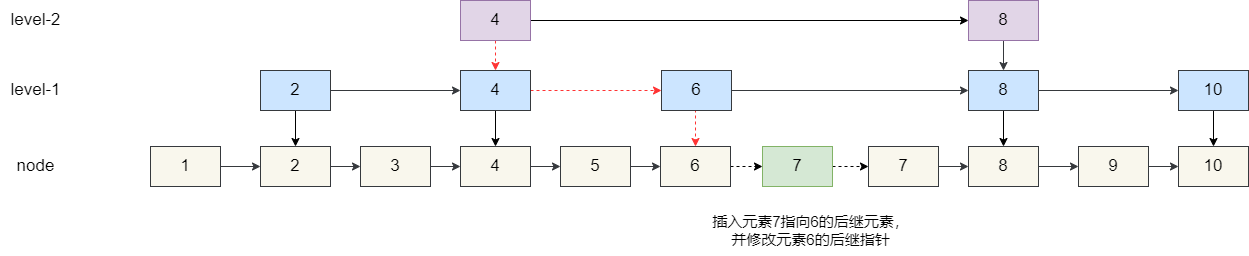
对应的添加也是一个道理,假如我们需要在这个有序集合中添加一个元素 7,那么我们就需要通过跳表找到 **小于元素 7 的最大值**,也就是下图元素 6 的位置,将其插入到元素 6 的后面,让元素 6 的索引指向新插入的节点 7,其工作流程如下:
|
||
|
||
1. 从 2 级索引开始定位到了元素 4 的索引。
|
||
2. 查看索引 4 的后继索引为 8,索引向下推进。
|
||
3. 来到 1 级索引,发现索引 4 后继索引为 6,小于插入元素 7,指针推进到索引 6 位置。
|
||
4. 继续比较 6 的后继节点为索引 8,大于元素 7,索引继续向下。
|
||
5. 最终我们来到 6 的原始节点,发现其后继节点为 7,指针没有继续向下的空间,自此我们可知元素 6 就是小于插入元素 7 的最大值,于是便将元素 7 插入。
|
||
|
||
|
||
|
||
这里我们又面临一个问题,我们是否需要为元素 7 建立索引,索引多高合适?
|
||
|
||
我们上文提到,理想情况是每一层索引是下一层元素个数的二分之一,假设我们的总共有 16 个元素,对应各级索引元素个数应该是:
|
||
|
||
```bash
|
||
1. 一级索引:16/2=8
|
||
2. 二级索引:8/2 =4
|
||
3. 三级索引:4/2=2
|
||
```
|
||
|
||
由此我们用数学归纳法可知:
|
||
|
||
```bash
|
||
1. 一级索引:16/2=16/2^1=8
|
||
2. 二级索引:8/2 => 16/2^2 =4
|
||
3. 三级索引:4/2=>16/2^3=2
|
||
```
|
||
|
||
假设元素个数为 n,那么对应 k 层索引的元素个数 r 计算公式为:
|
||
|
||
```bash
|
||
r=n/2^k
|
||
```
|
||
|
||
同理我们再来推断以下索引的最大高度,一般来说最高级索引的元素个数为 2,我们设元素总个数为 n,索引高度为 h,代入上述公式可得:
|
||
|
||
```bash
|
||
2= n/2^h
|
||
=> 2*2^h=n
|
||
=> 2^(h+1)=n
|
||
=> h+1=log2^n
|
||
=> h=log2^n -1
|
||
```
|
||
|
||
而 Redis 又是内存数据库,我们假设元素最大个数是 **65536**,我们把 **65536** 代入上述公式可知最大高度为 16。所以我们建议添加一个元素后为其建立的索引高度不超过 16。
|
||
|
||
因为我们要求尽可能保证每一个上级索引都是下级索引的一半,在实现高度生成算法时,我们可以这样设计:
|
||
|
||
1. 跳表的高度计算从原始链表开始,即默认情况下插入的元素的高度为 1,代表没有索引,只有元素节点。
|
||
2. 设计一个为插入元素生成节点索引高度 level 的方法。
|
||
3. 进行一次随机运算,随机数值范围为 0-1 之间。
|
||
4. 如果随机数大于 0.5 则为当前元素添加一级索引,自此我们保证生成一级索引的概率为 **50%**,这也就保证了 1 级索引理想情况下只有一半的元素会生成索引。
|
||
5. 同理后续每次随机算法得到的值大于 0.5 时,我们的索引高度就加 1,这样就可以保证节点生成的 2 级索引概率为 **25%**,3 级索引为 **12.5%**……
|
||
|
||
我们回过头,上述插入 7 之后,我们通过随机算法得到 2,即要为其建立 1 级索引:
|
||
|
||

|
||
|
||
最后我们再来说说删除,假设我们这里要删除元素 10,我们必须定位到当前跳表 **各层** 元素小于 10 的最大值,索引执行步骤为:
|
||
|
||
1. 2 级索引 4 的后继节点为 8,指针推进。
|
||
2. 索引 8 无后继节点,该层无要删除的元素,指针直接向下。
|
||
3. 1 级索引 8 后继节点为 10,说明 1 级索引 8 在进行删除时需要将自己的指针和 1 级索引 10 断开联系,将 10 删除。
|
||
4. 1 级索引完成定位后,指针向下,后继节点为 9,指针推进。
|
||
5. 9 的后继节点为 10,同理需要让其指向 null,将 10 删除。
|
||
|
||

|
||
|
||
### 模板定义
|
||
|
||
有了整体的思路之后,我们可以开始实现一个跳表了,首先定义一下跳表中的节点 **Node**,从上文的演示中可以看出每一个 **Node** 都包含以下几个元素:
|
||
|
||
1. 存储的 **value** 值。
|
||
2. 后继节点的地址。
|
||
3. 多级索引。
|
||
|
||
为了更方便统一管理 **Node** 后继节点地址和多级索引指向的元素地址,笔者在 **Node** 中设置了一个 **forwards** 数组,用于记录原始链表节点的后继节点和多级索引的后继节点指向。
|
||
|
||
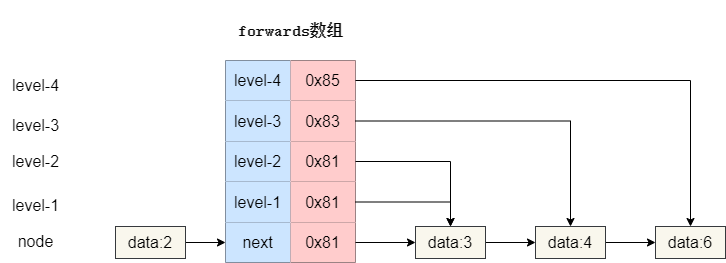
以下图为例,我们 **forwards** 数组长度为 5,其中 **索引 0** 记录的是原始链表节点的后继节点地址,而其余自底向上表示从 1 级索引到 4 级索引的后继节点指向。
|
||
|
||
|
||
|
||
于是我们的就有了这样一个代码定义,可以看出笔者对于数组的长度设置为固定的 16 **(上文的推算最大高度建议是 16)**,默认 **data** 为 -1,节点最大高度 **maxLevel** 初始化为 1,注意这个 **maxLevel** 的值代表原始链表加上索引的总高度。
|
||
|
||
```java
|
||
/**
|
||
* 跳表索引最大高度为16
|
||
*/
|
||
private static final int MAX_LEVEL = 16;
|
||
|
||
class Node {
|
||
private int data = -1;
|
||
private Node[] forwards = new Node[MAX_LEVEL];
|
||
private int maxLevel = 0;
|
||
|
||
}
|
||
```
|
||
|
||
### 元素添加
|
||
|
||
定义好节点之后,我们先实现以下元素的添加,添加元素时首先自然是设置 **data**,这一步我们直接根据将传入的 **value** 设置到 **data** 上即可。
|
||
|
||
然后就是高度 **maxLevel** 的设置 ,我们在上文也已经给出了思路,默认高度为 1,即只有一个原始链表节点,通过随机算法每次大于 0.5 索引高度加 1,由此我们得出高度计算的算法 `randomLevel()`:
|
||
|
||
```java
|
||
/**
|
||
* 理论来讲,一级索引中元素个数应该占原始数据的 50%,二级索引中元素个数占 25%,三级索引12.5%,一直到最顶层。
|
||
* 因为这里每一层的晋升概率是 50%。对于每一个新插入的节点,都需要调用 randomLevel 生成一个合理的层数。
|
||
* 该 randomLevel 方法会随机生成 1~MAX_LEVEL 之间的数,且:
|
||
* 50%的概率返回 1
|
||
* 25%的概率返回 2
|
||
* 12.5%的概率返回 3......
|
||
* @return
|
||
*/
|
||
private int randomLevel() {
|
||
int level = 1;
|
||
while (Math.random() > PROB && level < MAX_LEVEL) {
|
||
++level;
|
||
}
|
||
return level;
|
||
}
|
||
```
|
||
|
||
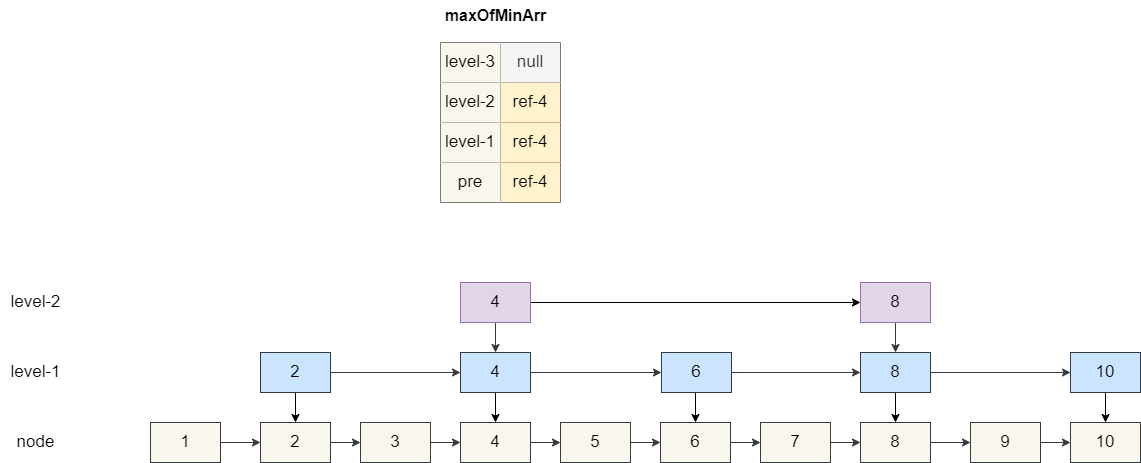
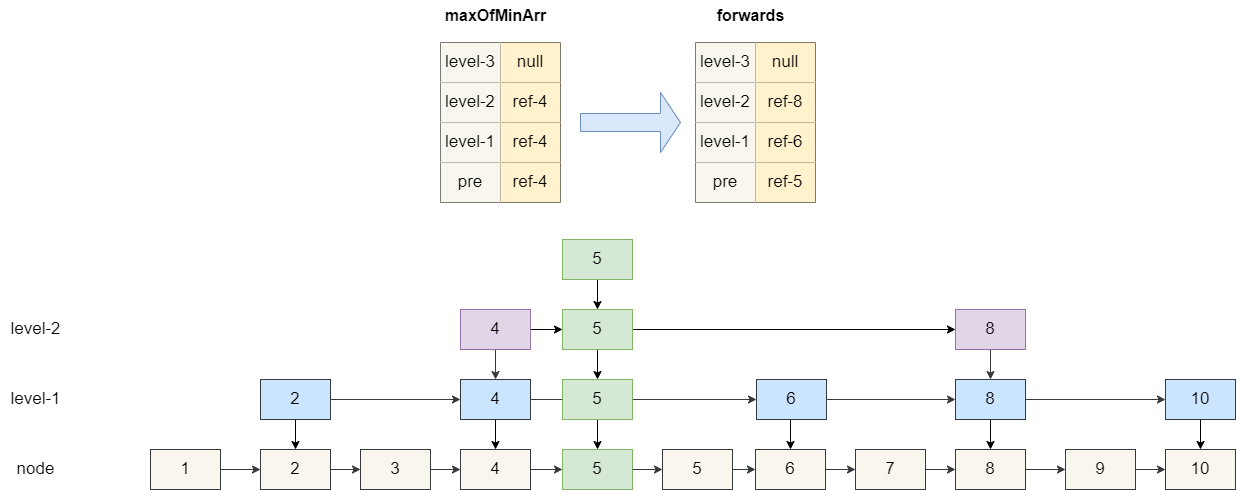
然后再设置当前要插入的 **Node** 和 **Node** 索引的后继节点地址,这一步稍微复杂一点,我们假设当前节点的高度为 4,即 1 个节点加 3 个索引,所以我们创建一个长度为 4 的数组 **maxOfMinArr**,遍历各级索引节点中小于当前 **value** 的最大值。
|
||
|
||
假设我们要插入的 **value** 为 5,我们的数组查找结果当前节点的前驱节点和 1 级索引、2 级索引的前驱节点都为 4,三级索引为空。
|
||
|
||
|
||
|
||
然后我们基于这个数组 **maxOfMinArr** 定位到各级的后继节点,让插入的元素 5 指向这些后继节点,而 **maxOfMinArr** 指向 5,结果如下图:
|
||
|
||
|
||
|
||
转化成代码就是下面这个形式,是不是很简单呢?我们继续:
|
||
|
||
```java
|
||
/**
|
||
* 默认情况下的高度为1,即只有自己一个节点
|
||
*/
|
||
private int levelCount = 1;
|
||
|
||
/**
|
||
* 跳表最底层的节点,即头节点
|
||
*/
|
||
private Node h = new Node();
|
||
|
||
public void add(int value) {
|
||
|
||
//随机生成高度
|
||
int level = randomLevel();
|
||
|
||
Node newNode = new Node();
|
||
newNode.data = value;
|
||
newNode.maxLevel = level;
|
||
|
||
//创建一个node数组,用于记录小于当前value的最大值
|
||
Node[] maxOfMinArr = new Node[level];
|
||
//默认情况下指向头节点
|
||
for (int i = 0; i < level; i++) {
|
||
maxOfMinArr[i] = h;
|
||
}
|
||
|
||
//基于上述结果拿到当前节点的后继节点
|
||
Node p = h;
|
||
for (int i = level - 1; i >= 0; i--) {
|
||
while (p.forwards[i] != null && p.forwards[i].data < value) {
|
||
p = p.forwards[i];
|
||
}
|
||
maxOfMinArr[i] = p;
|
||
}
|
||
|
||
//更新前驱节点的后继节点为当前节点newNode
|
||
for (int i = 0; i < level; i++) {
|
||
newNode.forwards[i] = maxOfMinArr[i].forwards[i];
|
||
maxOfMinArr[i].forwards[i] = newNode;
|
||
}
|
||
|
||
//如果当前newNode高度大于跳表最高高度则更新levelCount
|
||
if (levelCount < level) {
|
||
levelCount = level;
|
||
}
|
||
|
||
}
|
||
```
|
||
|
||
### 元素查询
|
||
|
||
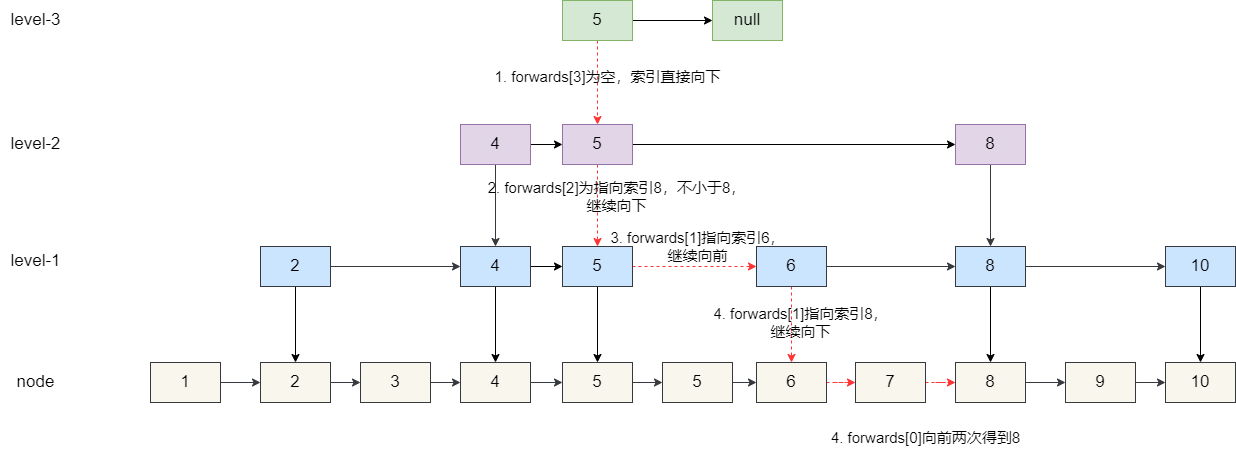
查询逻辑比较简单,从跳表最高级的索引开始定位找到小于要查的 value 的最大值,以下图为例,我们希望查找到节点 8:
|
||
|
||
1. 跳表的 3 级索引首先找找到 5 的索引,5 的 3 级索引 **forwards[3]** 指向空,索引直接向下。
|
||
2. 来到 5 的 2 级索引,其后继 **forwards[2]** 指向 8,继续向下。
|
||
3. 5 的 1 级索引 **forwards[1]** 指向索引 6,继续向前。
|
||
4. 索引 6 的 **forwards[1]** 指向索引 8,继续向下。
|
||
5. 我们在原始节点向前找到节点 7。
|
||
6. 节点 7 后续就是节点 8,继续向前为节点 8,无法继续向下,结束搜寻。
|
||
7. 判断 7 的前驱,等于 8,查找结束。
|
||
|
||
|
||
|
||
所以我们的代码实现也很上述步骤差不多,从最高级索引开始向前查找,如果不为空且小于要查找的值,则继续向前搜寻,遇到不小于的节点则继续向下,如此往复,直到得到当前跳表中小于查找值的最大节点,查看其前驱是否等于要查找的值:
|
||
|
||
```java
|
||
public Node get(int value) {
|
||
Node p = h;
|
||
//找到小于value的最大值
|
||
for (int i = levelCount - 1; i >= 0; i--) {
|
||
while (p.forwards[i] != null && p.forwards[i].data < value) {
|
||
p = p.forwards[i];
|
||
}
|
||
}
|
||
//如果p的前驱节点等于value则直接返回
|
||
if (p.forwards[0] != null && p.forwards[0].data == value) {
|
||
return p.forwards[0];
|
||
}
|
||
|
||
return null;
|
||
}
|
||
```
|
||
|
||
### 元素删除
|
||
|
||
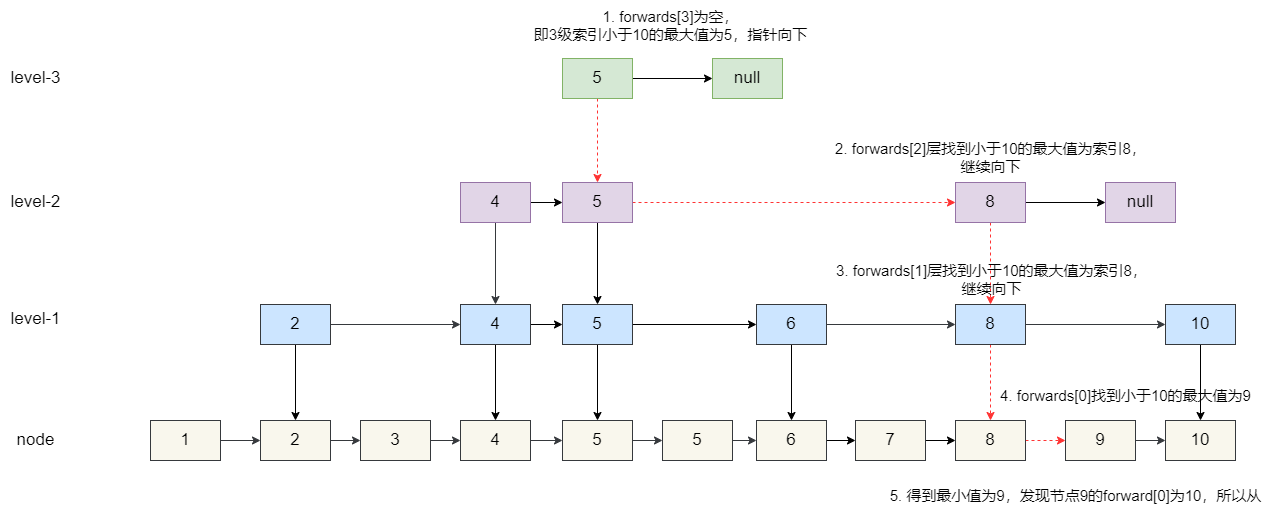
最后是删除逻辑,需要查找各层级小于要删除节点的最大值,假设我们要删除 10:
|
||
|
||
1. 3 级索引得到小于 10 的最大值为 5,继续向下。
|
||
2. 2 级索引从索引 5 开始查找,发现小于 10 的最大值为 8,继续向下。
|
||
3. 同理 1 级索引得到 8,继续向下。
|
||
4. 原始节点找到 9。
|
||
5. 从最高级索引开始,查看每个小于 10 的节点后继节点是否为 10,如果等于 10,则让这个节点指向 10 的后继节点,将节点 10 及其索引交由 GC 回收。
|
||
|
||
|
||
|
||
```java
|
||
/**
|
||
* 删除
|
||
*
|
||
* @param value
|
||
*/
|
||
public void delete(int value) {
|
||
Node p = h;
|
||
//找到各级节点小于value的最大值
|
||
Node[] updateArr = new Node[levelCount];
|
||
for (int i = levelCount - 1; i >= 0; i--) {
|
||
while (p.forwards[i] != null && p.forwards[i].data < value) {
|
||
p = p.forwards[i];
|
||
}
|
||
updateArr[i] = p;
|
||
}
|
||
//查看原始层节点前驱是否等于value,若等于则说明存在要删除的值
|
||
if (p.forwards[0] != null && p.forwards[0].data == value) {
|
||
//从最高级索引开始查看其前驱是否等于value,若等于则将当前节点指向value节点的后继节点
|
||
for (int i = levelCount - 1; i >= 0; i--) {
|
||
if (updateArr[i].forwards[i] != null && updateArr[i].forwards[i].data == value) {
|
||
updateArr[i].forwards[i] = updateArr[i].forwards[i].forwards[i];
|
||
}
|
||
}
|
||
}
|
||
|
||
//从最高级开始查看是否有一级索引为空,若为空则层级减1
|
||
while (levelCount > 1 && h.forwards[levelCount - 1] == null) {
|
||
levelCount--;
|
||
}
|
||
|
||
}
|
||
```
|
||
|
||
### 完整代码以及测试
|
||
|
||
完整代码如下,读者可自行参阅:
|
||
|
||
```java
|
||
public class SkipList {
|
||
|
||
/**
|
||
* 跳表索引最大高度为16
|
||
*/
|
||
private static final int MAX_LEVEL = 16;
|
||
|
||
/**
|
||
* 每个节点添加一层索引高度的概率为二分之一
|
||
*/
|
||
private static final float PROB = 0.5f;
|
||
|
||
/**
|
||
* 默认情况下的高度为1,即只有自己一个节点
|
||
*/
|
||
private int levelCount = 1;
|
||
|
||
/**
|
||
* 跳表最底层的节点,即头节点
|
||
*/
|
||
private Node h = new Node();
|
||
|
||
public SkipList() {}
|
||
|
||
public class Node {
|
||
private int data = -1;
|
||
/**
|
||
*
|
||
*/
|
||
private Node[] forwards = new Node[MAX_LEVEL];
|
||
private int maxLevel = 0;
|
||
|
||
@Override
|
||
public String toString() {
|
||
return "Node{" +
|
||
"data=" + data +
|
||
", maxLevel=" + maxLevel +
|
||
'}';
|
||
}
|
||
}
|
||
|
||
public void add(int value) {
|
||
|
||
//随机生成高度
|
||
int level = randomLevel();
|
||
|
||
Node newNode = new Node();
|
||
newNode.data = value;
|
||
newNode.maxLevel = level;
|
||
|
||
//创建一个node数组,用于记录小于当前value的最大值
|
||
Node[] maxOfMinArr = new Node[level];
|
||
//默认情况下指向头节点
|
||
for (int i = 0; i < level; i++) {
|
||
maxOfMinArr[i] = h;
|
||
}
|
||
|
||
//基于上述结果拿到当前节点的后继节点
|
||
Node p = h;
|
||
for (int i = level - 1; i >= 0; i--) {
|
||
while (p.forwards[i] != null && p.forwards[i].data < value) {
|
||
p = p.forwards[i];
|
||
}
|
||
maxOfMinArr[i] = p;
|
||
}
|
||
|
||
//更新前驱节点的后继节点为当前节点newNode
|
||
for (int i = 0; i < level; i++) {
|
||
newNode.forwards[i] = maxOfMinArr[i].forwards[i];
|
||
maxOfMinArr[i].forwards[i] = newNode;
|
||
}
|
||
|
||
//如果当前newNode高度大于跳表最高高度则更新levelCount
|
||
if (levelCount < level) {
|
||
levelCount = level;
|
||
}
|
||
|
||
}
|
||
|
||
/**
|
||
* 理论来讲,一级索引中元素个数应该占原始数据的 50%,二级索引中元素个数占 25%,三级索引12.5% ,一直到最顶层。
|
||
* 因为这里每一层的晋升概率是 50%。对于每一个新插入的节点,都需要调用 randomLevel 生成一个合理的层数。
|
||
* 该 randomLevel 方法会随机生成 1~MAX_LEVEL 之间的数,且 :
|
||
* 50%的概率返回 1
|
||
* 25%的概率返回 2
|
||
* 12.5%的概率返回 3 ...
|
||
* @return
|
||
*/
|
||
private int randomLevel() {
|
||
int level = 1;
|
||
while (Math.random() > PROB && level < MAX_LEVEL) {
|
||
++level;
|
||
}
|
||
return level;
|
||
}
|
||
|
||
public Node get(int value) {
|
||
Node p = h;
|
||
//找到小于value的最大值
|
||
for (int i = levelCount - 1; i >= 0; i--) {
|
||
while (p.forwards[i] != null && p.forwards[i].data < value) {
|
||
p = p.forwards[i];
|
||
}
|
||
}
|
||
//如果p的前驱节点等于value则直接返回
|
||
if (p.forwards[0] != null && p.forwards[0].data == value) {
|
||
return p.forwards[0];
|
||
}
|
||
|
||
return null;
|
||
}
|
||
|
||
/**
|
||
* 删除
|
||
*
|
||
* @param value
|
||
*/
|
||
public void delete(int value) {
|
||
Node p = h;
|
||
//找到各级节点小于value的最大值
|
||
Node[] updateArr = new Node[levelCount];
|
||
for (int i = levelCount - 1; i >= 0; i--) {
|
||
while (p.forwards[i] != null && p.forwards[i].data < value) {
|
||
p = p.forwards[i];
|
||
}
|
||
updateArr[i] = p;
|
||
}
|
||
//查看原始层节点前驱是否等于value,若等于则说明存在要删除的值
|
||
if (p.forwards[0] != null && p.forwards[0].data == value) {
|
||
//从最高级索引开始查看其前驱是否等于value,若等于则将当前节点指向value节点的后继节点
|
||
for (int i = levelCount - 1; i >= 0; i--) {
|
||
if (updateArr[i].forwards[i] != null && updateArr[i].forwards[i].data == value) {
|
||
updateArr[i].forwards[i] = updateArr[i].forwards[i].forwards[i];
|
||
}
|
||
}
|
||
}
|
||
|
||
//从最高级开始查看是否有一级索引为空,若为空则层级减1
|
||
while (levelCount > 1 && h.forwards[levelCount - 1] == null) {
|
||
levelCount--;
|
||
}
|
||
|
||
}
|
||
|
||
public void printAll() {
|
||
Node p = h;
|
||
//基于最底层的非索引层进行遍历,只要后继节点不为空,则速速出当前节点,并移动到后继节点
|
||
while (p.forwards[0] != null) {
|
||
System.out.println(p.forwards[0]);
|
||
p = p.forwards[0];
|
||
}
|
||
|
||
}
|
||
|
||
}
|
||
```
|
||
|
||
对应测试代码和输出结果如下:
|
||
|
||
```java
|
||
public static void main(String[] args) {
|
||
SkipList skipList = new SkipList();
|
||
for (int i = 0; i < 24; i++) {
|
||
skipList.add(i);
|
||
}
|
||
|
||
System.out.println("**********输出添加结果**********");
|
||
skipList.printAll();
|
||
|
||
SkipList.Node node = skipList.get(22);
|
||
System.out.println("**********查询结果:" + node+" **********");
|
||
|
||
skipList.delete(22);
|
||
System.out.println("**********删除结果**********");
|
||
skipList.printAll();
|
||
|
||
|
||
}
|
||
```
|
||
|
||
输出结果:
|
||
|
||
```bash
|
||
**********输出添加结果**********
|
||
Node{data=0, maxLevel=2}
|
||
Node{data=1, maxLevel=3}
|
||
Node{data=2, maxLevel=1}
|
||
Node{data=3, maxLevel=1}
|
||
Node{data=4, maxLevel=2}
|
||
Node{data=5, maxLevel=2}
|
||
Node{data=6, maxLevel=2}
|
||
Node{data=7, maxLevel=2}
|
||
Node{data=8, maxLevel=4}
|
||
Node{data=9, maxLevel=1}
|
||
Node{data=10, maxLevel=1}
|
||
Node{data=11, maxLevel=1}
|
||
Node{data=12, maxLevel=1}
|
||
Node{data=13, maxLevel=1}
|
||
Node{data=14, maxLevel=1}
|
||
Node{data=15, maxLevel=3}
|
||
Node{data=16, maxLevel=4}
|
||
Node{data=17, maxLevel=2}
|
||
Node{data=18, maxLevel=1}
|
||
Node{data=19, maxLevel=1}
|
||
Node{data=20, maxLevel=1}
|
||
Node{data=21, maxLevel=3}
|
||
Node{data=22, maxLevel=1}
|
||
Node{data=23, maxLevel=1}
|
||
**********查询结果:Node{data=22, maxLevel=1} **********
|
||
**********删除结果**********
|
||
Node{data=0, maxLevel=2}
|
||
Node{data=1, maxLevel=3}
|
||
Node{data=2, maxLevel=1}
|
||
Node{data=3, maxLevel=1}
|
||
Node{data=4, maxLevel=2}
|
||
Node{data=5, maxLevel=2}
|
||
Node{data=6, maxLevel=2}
|
||
Node{data=7, maxLevel=2}
|
||
Node{data=8, maxLevel=4}
|
||
Node{data=9, maxLevel=1}
|
||
Node{data=10, maxLevel=1}
|
||
Node{data=11, maxLevel=1}
|
||
Node{data=12, maxLevel=1}
|
||
Node{data=13, maxLevel=1}
|
||
Node{data=14, maxLevel=1}
|
||
Node{data=15, maxLevel=3}
|
||
Node{data=16, maxLevel=4}
|
||
Node{data=17, maxLevel=2}
|
||
Node{data=18, maxLevel=1}
|
||
Node{data=19, maxLevel=1}
|
||
Node{data=20, maxLevel=1}
|
||
Node{data=21, maxLevel=3}
|
||
Node{data=23, maxLevel=1}
|
||
```
|
||
|
||
**Redis 跳表的特点**:
|
||
|
||
1. 采用**双向链表**,不同于上面的示例,存在一个回退指针。主要用于简化操作,例如删除某个元素时,还需要找到该元素的前驱节点,使用回退指针会非常方便。
|
||
2. `score` 值可以重复,如果 `score` 值一样,则按照 ele(节点存储的值,为 sds)字典排序。
|
||
3. Redis 跳跃表默认允许最大的层数是 32,被源码中 `ZSKIPLIST_MAXLEVEL` 定义。
|
||
|
||
## 和其余三种数据结构的比较
|
||
|
||
最后,我们再来回答一下文章开头的那道面试题: “Redis 的有序集合底层为什么要用跳表,而不用平衡树、红黑树或者 B+树?”。
|
||
|
||
### 平衡树 vs 跳表
|
||
|
||
先来说说它和平衡树的比较,平衡树我们又会称之为 **AVL 树**,是一个严格的平衡二叉树,平衡条件必须满足(所有节点的左右子树高度差不超过 1,即平衡因子为范围为 `[-1,1]`)。平衡树的插入、删除和查询的时间复杂度和跳表一样都是 **O(log n)**。
|
||
|
||
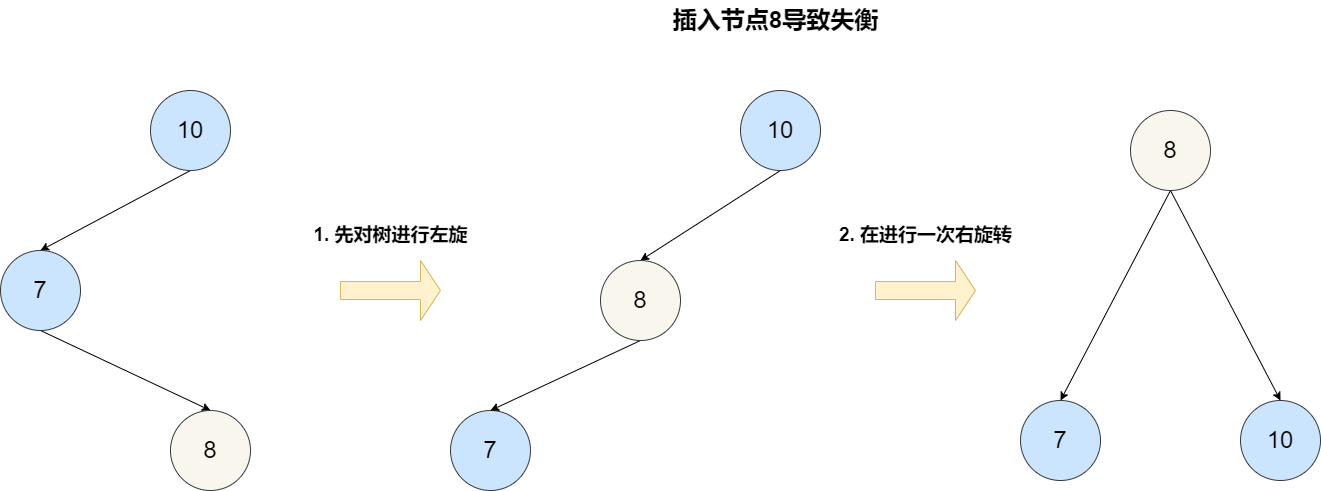
对于范围查询来说,它也可以通过中序遍历的方式达到和跳表一样的效果。但是它的每一次插入或者删除操作都需要保证整颗树左右节点的绝对平衡,只要不平衡就要通过旋转操作来保持平衡,这个过程是比较耗时的。
|
||
|
||
|
||
|
||
跳表诞生的初衷就是为了克服平衡树的一些缺点,跳表的发明者在论文 [《Skip lists: a probabilistic alternative to balanced trees》](https://15721.courses.cs.cmu.edu/spring2018/papers/08-oltpindexes1/pugh-skiplists-cacm1990.pdf) 中有详细提到:
|
||
|
||

|
||
|
||
> Skip lists are a data structure that can be used in place of balanced trees. Skip lists use probabilistic balancing rather than strictly enforced balancing and as a result the algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees.
|
||
>
|
||
> 跳表是一种可以用来代替平衡树的数据结构。跳表使用概率平衡而不是严格强制的平衡,因此,跳表中的插入和删除算法比平衡树的等效算法简单得多,速度也快得多。
|
||
|
||
笔者这里也贴出了 AVL 树插入操作的核心代码,可以看出每一次添加操作都需要进行一次递归定位插入位置,然后还需要根据回溯到根节点检查沿途的各层节点是否失衡,再通过旋转节点的方式进行调整。
|
||
|
||
```java
|
||
// 向二分搜索树中添加新的元素(key, value)
|
||
public void add(K key, V value) {
|
||
root = add(root, key, value);
|
||
}
|
||
|
||
// 向以node为根的二分搜索树中插入元素(key, value),递归算法
|
||
// 返回插入新节点后二分搜索树的根
|
||
private Node add(Node node, K key, V value) {
|
||
|
||
if (node == null) {
|
||
size++;
|
||
return new Node(key, value);
|
||
}
|
||
|
||
if (key.compareTo(node.key) < 0)
|
||
node.left = add(node.left, key, value);
|
||
else if (key.compareTo(node.key) > 0)
|
||
node.right = add(node.right, key, value);
|
||
else // key.compareTo(node.key) == 0
|
||
node.value = value;
|
||
|
||
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
|
||
|
||
int balanceFactor = getBalanceFactor(node);
|
||
|
||
// LL型需要右旋
|
||
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
|
||
return rightRotate(node);
|
||
}
|
||
|
||
//RR型失衡需要左旋
|
||
if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
|
||
return leftRotate(node);
|
||
}
|
||
|
||
//LR需要先左旋成LL型,然后再右旋
|
||
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
|
||
node.left = leftRotate(node.left);
|
||
return rightRotate(node);
|
||
}
|
||
|
||
//RL
|
||
if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
|
||
node.right = rightRotate(node.right);
|
||
return leftRotate(node);
|
||
}
|
||
return node;
|
||
}
|
||
```
|
||
|
||
### 红黑树 vs 跳表
|
||
|
||
红黑树(Red Black Tree)也是一种自平衡二叉查找树,它的查询性能略微逊色于 AVL 树,但插入和删除效率更高。红黑树的插入、删除和查询的时间复杂度和跳表一样都是 **O(log n)**。
|
||
|
||
红黑树是一个 **黑平衡树**,即从任意节点到另外一个叶子叶子节点,它所经过的黑节点是一样的。当对它进行插入操作时,需要通过旋转和染色(红黑变换)来保证黑平衡。不过,相较于 AVL 树为了维持平衡的开销要小一些。关于红黑树的详细介绍,可以查看这篇文章:[红黑树](https://javaguide.cn/cs-basics/data-structure/red-black-tree.html)。
|
||
|
||
相比较于红黑树来说,跳表的实现也更简单一些。并且,按照区间来查找数据这个操作,红黑树的效率没有跳表高。
|
||
|
||

|
||
|
||
对应红黑树添加的核心代码如下,读者可自行参阅理解:
|
||
|
||
```java
|
||
private Node < K, V > add(Node < K, V > node, K key, V val) {
|
||
|
||
if (node == null) {
|
||
size++;
|
||
return new Node(key, val);
|
||
|
||
}
|
||
|
||
if (key.compareTo(node.key) < 0) {
|
||
node.left = add(node.left, key, val);
|
||
} else if (key.compareTo(node.key) > 0) {
|
||
node.right = add(node.right, key, val);
|
||
} else {
|
||
node.val = val;
|
||
}
|
||
|
||
//左节点不为红,右节点为红,左旋
|
||
if (isRed(node.right) && !isRed(node.left)) {
|
||
node = leftRotate(node);
|
||
}
|
||
|
||
//左链右旋
|
||
if (isRed(node.left) && isRed(node.left.left)) {
|
||
node = rightRotate(node);
|
||
}
|
||
|
||
//颜色翻转
|
||
if (isRed(node.left) && isRed(node.right)) {
|
||
flipColors(node);
|
||
}
|
||
|
||
return node;
|
||
}
|
||
```
|
||
|
||
### B+树 vs 跳表
|
||
|
||
想必使用 MySQL 的读者都知道 B+树这个数据结构,B+树是一种常用的数据结构,具有以下特点:
|
||
|
||
1. **多叉树结构**:它是一棵多叉树,每个节点可以包含多个子节点,减小了树的高度,查询效率高。
|
||
2. **存储效率高**:其中非叶子节点存储多个 key,叶子节点存储 value,使得每个节点更够存储更多的键,根据索引进行范围查询时查询效率更高。-
|
||
3. **平衡性**:它是绝对的平衡,即树的各个分支高度相差不大,确保查询和插入时间复杂度为 **O(log n)** 。
|
||
4. **顺序访问**:叶子节点间通过链表指针相连,范围查询表现出色。
|
||
5. **数据均匀分布**:B+树插入时可能会导致数据重新分布,使得数据在整棵树分布更加均匀,保证范围查询和删除效率。
|
||
|
||

|
||
|
||
所以,B+树更适合作为数据库和文件系统中常用的索引结构之一,它的核心思想是通过可能少的 IO 定位到尽可能多的索引来获得查询数据。对于 Redis 这种内存数据库来说,它对这些并不感冒,因为 Redis 作为内存数据库它不可能存储大量的数据,所以对于索引不需要通过 B+树这种方式进行维护,只需按照概率进行随机维护即可,节约内存。而且使用跳表实现 zset 时相较前者来说更简单一些,在进行插入时只需通过索引将数据插入到链表中合适的位置再随机维护一定高度的索引即可,也不需要像 B+树那样插入时发现失衡时还需要对节点分裂与合并。
|
||
|
||
### Redis 作者给出的理由
|
||
|
||
当然我们也可以通过 Redis 的作者自己给出的理由:
|
||
|
||
> There are a few reasons:
|
||
> 1、They are not very memory intensive. It's up to you basically. Changing parameters about the probability of a node to have a given number of levels will make then less memory intensive than btrees.
|
||
> 2、A sorted set is often target of many ZRANGE or ZREVRANGE operations, that is, traversing the skip list as a linked list. With this operation the cache locality of skip lists is at least as good as with other kind of balanced trees.
|
||
> 3、They are simpler to implement, debug, and so forth. For instance thanks to the skip list simplicity I received a patch (already in Redis master) with augmented skip lists implementing ZRANK in O(log(N)). It required little changes to the code.
|
||
|
||
翻译过来的意思就是:
|
||
|
||
> 有几个原因:
|
||
>
|
||
> 1、它们不是很占用内存。这主要取决于你。改变节点拥有给定层数的概率的参数,会使它们比 B 树更节省内存。
|
||
>
|
||
> 2、有序集合经常是许多 ZRANGE 或 ZREVRANGE 操作的目标,也就是说,以链表的方式遍历跳表。通过这种操作,跳表的缓存局部性至少和其他类型的平衡树一样好。
|
||
>
|
||
> 3、它们更容易实现、调试等等。例如,由于跳表的简单性,我收到了一个补丁(已经在 Redis 主分支中),用增强的跳表实现了 O(log(N))的 ZRANK。它只需要对代码做很少的修改。
|
||
|
||
## 小结
|
||
|
||
本文通过大量篇幅介绍跳表的工作原理和实现,帮助读者更进一步的熟悉跳表这一数据结构的优劣,最后再结合各个数据结构操作的特点进行比对,从而帮助读者更好的理解这道面试题,建议读者实现理解跳表时,尽可能配合执笔模拟来了解跳表的增删改查详细过程。
|
||
|
||
## 参考
|
||
|
||
- 为啥 redis 使用跳表(skiplist)而不是使用 red-black?:<https://www.zhihu.com/question/20202931/answer/16086538>
|
||
- Skip List--跳表(全网最详细的跳表文章没有之一):<https://www.jianshu.com/p/9d8296562806>
|
||
- Redis 对象与底层数据结构详解:<https://blog.csdn.net/shark_chili3007/article/details/104171986>
|
||
- Redis 有序集合(sorted set):<https://www.runoob.com/redis/redis-sorted-sets.html>
|
||
- 红黑树和跳表比较:<https://zhuanlan.zhihu.com/p/576984787>
|
||
- 为什么 redis 的 zset 用跳跃表而不用 b+ tree?:<https://blog.csdn.net/f80407515/article/details/129136998>
|