mirror of
https://github.com/Snailclimb/JavaGuide
synced 2025-06-16 18:10:13 +08:00
684 lines
22 KiB
Markdown
684 lines
22 KiB
Markdown
---
|
||
title: 剑指offer部分编程题
|
||
category: 计算机基础
|
||
tag:
|
||
- 算法
|
||
---
|
||
|
||
## 斐波那契数列
|
||
|
||
**题目描述:**
|
||
|
||
大家都知道斐波那契数列,现在要求输入一个整数 n,请你输出斐波那契数列的第 n 项。
|
||
n<=39
|
||
|
||
**问题分析:**
|
||
|
||
可以肯定的是这一题通过递归的方式是肯定能做出来,但是这样会有一个很大的问题,那就是递归大量的重复计算会导致内存溢出。另外可以使用迭代法,用 fn1 和 fn2 保存计算过程中的结果,并复用起来。下面我会把两个方法示例代码都给出来并给出两个方法的运行时间对比。
|
||
|
||
**示例代码:**
|
||
|
||
采用迭代法:
|
||
|
||
```java
|
||
int Fibonacci(int number) {
|
||
if (number <= 0) {
|
||
return 0;
|
||
}
|
||
if (number == 1 || number == 2) {
|
||
return 1;
|
||
}
|
||
int first = 1, second = 1, third = 0;
|
||
for (int i = 3; i <= number; i++) {
|
||
third = first + second;
|
||
first = second;
|
||
second = third;
|
||
}
|
||
return third;
|
||
}
|
||
```
|
||
|
||
采用递归:
|
||
|
||
```java
|
||
public int Fibonacci(int n) {
|
||
if (n <= 0) {
|
||
return 0;
|
||
}
|
||
if (n == 1||n==2) {
|
||
return 1;
|
||
}
|
||
|
||
return Fibonacci(n - 2) + Fibonacci(n - 1);
|
||
}
|
||
```
|
||
|
||
## 跳台阶问题
|
||
|
||
**题目描述:**
|
||
|
||
一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
|
||
|
||
**问题分析:**
|
||
|
||
正常分析法:
|
||
|
||
> a.如果两种跳法,1 阶或者 2 阶,那么假定第一次跳的是一阶,那么剩下的是 n-1 个台阶,跳法是 f(n-1);
|
||
> b.假定第一次跳的是 2 阶,那么剩下的是 n-2 个台阶,跳法是 f(n-2)
|
||
> c.由 a,b 假设可以得出总跳法为: f(n) = f(n-1) + f(n-2)
|
||
> d.然后通过实际的情况可以得出:只有一阶的时候 f(1) = 1 ,只有两阶的时候可以有 f(2) = 2
|
||
|
||
找规律分析法:
|
||
|
||
> f(1) = 1, f(2) = 2, f(3) = 3, f(4) = 5, 可以总结出 f(n) = f(n-1) + f(n-2)的规律。但是为什么会出现这样的规律呢?假设现在 6 个台阶,我们可以从第 5 跳一步到 6,这样的话有多少种方案跳到 5 就有多少种方案跳到 6,另外我们也可以从 4 跳两步跳到 6,跳到 4 有多少种方案的话,就有多少种方案跳到 6,其他的不能从 3 跳到 6 什么的啦,所以最后就是 f(6) = f(5) + f(4);这样子也很好理解变态跳台阶的问题了。
|
||
|
||
**所以这道题其实就是斐波那契数列的问题。**
|
||
|
||
代码只需要在上一题的代码稍做修改即可。和上一题唯一不同的就是这一题的初始元素变为 1 2 3 5 8.....而上一题为 1 1 2 3 5 .......。另外这一题也可以用递归做,但是递归效率太低,所以我这里只给出了迭代方式的代码。
|
||
|
||
**示例代码:**
|
||
|
||
```java
|
||
int jumpFloor(int number) {
|
||
if (number <= 0) {
|
||
return 0;
|
||
}
|
||
if (number == 1) {
|
||
return 1;
|
||
}
|
||
if (number == 2) {
|
||
return 2;
|
||
}
|
||
int first = 1, second = 2, third = 0;
|
||
for (int i = 3; i <= number; i++) {
|
||
third = first + second;
|
||
first = second;
|
||
second = third;
|
||
}
|
||
return third;
|
||
}
|
||
```
|
||
|
||
## 变态跳台阶问题
|
||
|
||
**题目描述:**
|
||
|
||
一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级……它也可以跳上 n 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
|
||
|
||
**问题分析:**
|
||
|
||
假设 n>=2,第一步有 n 种跳法:跳 1 级、跳 2 级、到跳 n 级
|
||
跳 1 级,剩下 n-1 级,则剩下跳法是 f(n-1)
|
||
跳 2 级,剩下 n-2 级,则剩下跳法是 f(n-2)
|
||
......
|
||
跳 n-1 级,剩下 1 级,则剩下跳法是 f(1)
|
||
跳 n 级,剩下 0 级,则剩下跳法是 f(0)
|
||
所以在 n>=2 的情况下:
|
||
f(n)=f(n-1)+f(n-2)+...+f(1)
|
||
因为 f(n-1)=f(n-2)+f(n-3)+...+f(1)
|
||
所以 f(n)=2\*f(n-1) 又 f(1)=1,所以可得**f(n)=2^(number-1)**
|
||
|
||
**示例代码:**
|
||
|
||
```java
|
||
int JumpFloorII(int number) {
|
||
return 1 << --number;//2^(number-1)用位移操作进行,更快
|
||
}
|
||
```
|
||
|
||
**补充:**
|
||
|
||
java 中有三种移位运算符:
|
||
|
||
1. “<<” : **左移运算符**,等同于乘 2 的 n 次方
|
||
2. “>>”: **右移运算符**,等同于除 2 的 n 次方
|
||
3. “>>>” : **无符号右移运算符**,不管移动前最高位是 0 还是 1,右移后左侧产生的空位部分都以 0 来填充。与>>类似。
|
||
|
||
```java
|
||
int a = 16;
|
||
int b = a << 2;//左移2,等同于16 * 2的2次方,也就是16 * 4
|
||
int c = a >> 2;//右移2,等同于16 / 2的2次方,也就是16 / 4
|
||
```
|
||
|
||
## 二维数组查找
|
||
|
||
**题目描述:**
|
||
|
||
在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
|
||
|
||
**问题解析:**
|
||
|
||
这一道题还是比较简单的,我们需要考虑的是如何做,效率最快。这里有一种很好理解的思路:
|
||
|
||
> 矩阵是有序的,从左下角来看,向上数字递减,向右数字递增,
|
||
> 因此从左下角开始查找,当要查找数字比左下角数字大时。右移
|
||
> 要查找数字比左下角数字小时,上移。这样找的速度最快。
|
||
|
||
**示例代码:**
|
||
|
||
```java
|
||
public boolean Find(int target, int [][] array) {
|
||
//基本思路从左下角开始找,这样速度最快
|
||
int row = array.length-1;//行
|
||
int column = 0;//列
|
||
//当行数大于0,当前列数小于总列数时循环条件成立
|
||
while((row >= 0)&& (column< array[0].length)){
|
||
if(array[row][column] > target){
|
||
row--;
|
||
}else if(array[row][column] < target){
|
||
column++;
|
||
}else{
|
||
return true;
|
||
}
|
||
}
|
||
return false;
|
||
}
|
||
```
|
||
|
||
## 替换空格
|
||
|
||
**题目描述:**
|
||
|
||
请实现一个函数,将一个字符串中的空格替换成“%20”。例如,当字符串为 We Are Happy.则经过替换之后的字符串为 We%20Are%20Happy。
|
||
|
||
**问题分析:**
|
||
|
||
这道题不难,我们可以通过循环判断字符串的字符是否为空格,是的话就利用 append()方法添加追加“%20”,否则还是追加原字符。
|
||
|
||
或者最简单的方法就是利用:replaceAll(String regex,String replacement)方法了,一行代码就可以解决。
|
||
|
||
**示例代码:**
|
||
|
||
常规做法:
|
||
|
||
```java
|
||
public String replaceSpace(StringBuffer str) {
|
||
StringBuffer out = new StringBuffer();
|
||
for (int i = 0; i < str.toString().length(); i++) {
|
||
char b = str.charAt(i);
|
||
if(String.valueOf(b).equals(" ")){
|
||
out.append("%20");
|
||
}else{
|
||
out.append(b);
|
||
}
|
||
}
|
||
return out.toString();
|
||
}
|
||
```
|
||
|
||
一行代码解决:
|
||
|
||
```java
|
||
public String replaceSpace(StringBuffer str) {
|
||
//return str.toString().replaceAll(" ", "%20");
|
||
//public String replaceAll(String regex,String replacement)
|
||
//用给定的替换替换与给定的regular expression匹配的此字符串的每个子字符串。
|
||
//\ 转义字符. 如果你要使用 "\" 本身, 则应该使用 "\\". String类型中的空格用“\s”表示,所以我这里猜测"\\s"就是代表空格的意思
|
||
return str.toString().replaceAll("\\s", "%20");
|
||
}
|
||
```
|
||
|
||
## 数值的整数次方
|
||
|
||
**题目描述:**
|
||
|
||
给定一个 double 类型的浮点数 base 和 int 类型的整数 exponent。求 base 的 exponent 次方。
|
||
|
||
**问题解析:**
|
||
|
||
这道题算是比较麻烦和难一点的一个了。我这里采用的是**二分幂**思想,当然也可以采用**快速幂**。
|
||
更具剑指 offer 书中细节,该题的解题思路如下:1.当底数为 0 且指数<0 时,会出现对 0 求倒数的情况,需进行错误处理,设置一个全局变量; 2.判断底数是否等于 0,由于 base 为 double 型,所以不能直接用==判断 3.优化求幂函数(二分幂)。
|
||
当 n 为偶数,a^n =(a^n/2)_(a^n/2);
|
||
当 n 为奇数,a^n = a^[(n-1)/2] _ a^[(n-1)/2] \* a。时间复杂度 O(logn)
|
||
|
||
**时间复杂度**:O(logn)
|
||
|
||
**示例代码:**
|
||
|
||
```java
|
||
public class Solution {
|
||
boolean invalidInput=false;
|
||
public double Power(double base, int exponent) {
|
||
//如果底数等于0并且指数小于0
|
||
//由于base为double型,不能直接用==判断
|
||
if(equal(base,0.0)&&exponent<0){
|
||
invalidInput=true;
|
||
return 0.0;
|
||
}
|
||
int absexponent=exponent;
|
||
//如果指数小于0,将指数转正
|
||
if(exponent<0)
|
||
absexponent=-exponent;
|
||
//getPower方法求出base的exponent次方。
|
||
double res=getPower(base,absexponent);
|
||
//如果指数小于0,所得结果为上面求的结果的倒数
|
||
if(exponent<0)
|
||
res=1.0/res;
|
||
return res;
|
||
}
|
||
//比较两个double型变量是否相等的方法
|
||
boolean equal(double num1,double num2){
|
||
if(num1-num2>-0.000001&&num1-num2<0.000001)
|
||
return true;
|
||
else
|
||
return false;
|
||
}
|
||
//求出b的e次方的方法
|
||
double getPower(double b,int e){
|
||
//如果指数为0,返回1
|
||
if(e==0)
|
||
return 1.0;
|
||
//如果指数为1,返回b
|
||
if(e==1)
|
||
return b;
|
||
//e>>1相等于e/2,这里就是求a^n =(a^n/2)*(a^n/2)
|
||
double result=getPower(b,e>>1);
|
||
result*=result;
|
||
//如果指数n为奇数,则要再乘一次底数base
|
||
if((e&1)==1)
|
||
result*=b;
|
||
return result;
|
||
}
|
||
}
|
||
```
|
||
|
||
当然这一题也可以采用笨方法:累乘。不过这种方法的时间复杂度为 O(n),这样没有前一种方法效率高。
|
||
|
||
```java
|
||
// 使用累乘
|
||
public double powerAnother(double base, int exponent) {
|
||
double result = 1.0;
|
||
for (int i = 0; i < Math.abs(exponent); i++) {
|
||
result *= base;
|
||
}
|
||
if (exponent >= 0)
|
||
return result;
|
||
else
|
||
return 1 / result;
|
||
}
|
||
```
|
||
|
||
## 调整数组顺序使奇数位于偶数前面
|
||
|
||
**题目描述:**
|
||
|
||
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分,所有的偶数位于位于数组的后半部分,并保证奇数和奇数,偶数和偶数之间的相对位置不变。
|
||
|
||
**问题解析:**
|
||
|
||
这道题有挺多种解法的,给大家介绍一种我觉得挺好理解的方法:
|
||
我们首先统计奇数的个数假设为 n,然后新建一个等长数组,然后通过循环判断原数组中的元素为偶数还是奇数。如果是则从数组下标 0 的元素开始,把该奇数添加到新数组;如果是偶数则从数组下标为 n 的元素开始把该偶数添加到新数组中。
|
||
|
||
**示例代码:**
|
||
|
||
时间复杂度为 O(n),空间复杂度为 O(n)的算法
|
||
|
||
```java
|
||
public class Solution {
|
||
public void reOrderArray(int [] array) {
|
||
//如果数组长度等于0或者等于1,什么都不做直接返回
|
||
if(array.length==0||array.length==1)
|
||
return;
|
||
//oddCount:保存奇数个数
|
||
//oddBegin:奇数从数组头部开始添加
|
||
int oddCount=0,oddBegin=0;
|
||
//新建一个数组
|
||
int[] newArray=new int[array.length];
|
||
//计算出(数组中的奇数个数)开始添加元素
|
||
for(int i=0;i<array.length;i++){
|
||
if((array[i]&1)==1) oddCount++;
|
||
}
|
||
for(int i=0;i<array.length;i++){
|
||
//如果数为基数新数组从头开始添加元素
|
||
//如果为偶数就从oddCount(数组中的奇数个数)开始添加元素
|
||
if((array[i]&1)==1)
|
||
newArray[oddBegin++]=array[i];
|
||
else newArray[oddCount++]=array[i];
|
||
}
|
||
for(int i=0;i<array.length;i++){
|
||
array[i]=newArray[i];
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
## 链表中倒数第 k 个节点
|
||
|
||
**题目描述:**
|
||
|
||
输入一个链表,输出该链表中倒数第 k 个结点
|
||
|
||
**问题分析:**
|
||
|
||
**一句话概括:**
|
||
两个指针一个指针 p1 先开始跑,指针 p1 跑到 k-1 个节点后,另一个节点 p2 开始跑,当 p1 跑到最后时,p2 所指的指针就是倒数第 k 个节点。
|
||
|
||
**思想的简单理解:**
|
||
前提假设:链表的结点个数(长度)为 n。
|
||
规律一:要找到倒数第 k 个结点,需要向前走多少步呢?比如倒数第一个结点,需要走 n 步,那倒数第二个结点呢?很明显是向前走了 n-1 步,所以可以找到规律是找到倒数第 k 个结点,需要向前走 n-k+1 步。
|
||
|
||
**算法开始:**
|
||
|
||
1. 设两个都指向 head 的指针 p1 和 p2,当 p1 走了 k-1 步的时候,停下来。p2 之前一直不动。
|
||
2. p1 的下一步是走第 k 步,这个时候,p2 开始一起动了。至于为什么 p2 这个时候动呢?看下面的分析。
|
||
3. 当 p1 走到链表的尾部时,即 p1 走了 n 步。由于我们知道 p2 是在 p1 走了 k-1 步才开始动的,也就是说 p1 和 p2 永远差 k-1 步。所以当 p1 走了 n 步时,p2 走的应该是在 n-(k-1)步。即 p2 走了 n-k+1 步,此时巧妙的是 p2 正好指向的是规律一的倒数第 k 个结点处。
|
||
这样是不是很好理解了呢?
|
||
|
||
**考察内容:**
|
||
|
||
链表+代码的鲁棒性
|
||
|
||
**示例代码:**
|
||
|
||
```java
|
||
/*
|
||
//链表类
|
||
public class ListNode {
|
||
int val;
|
||
ListNode next = null;
|
||
|
||
ListNode(int val) {
|
||
this.val = val;
|
||
}
|
||
}*/
|
||
|
||
//时间复杂度O(n),一次遍历即可
|
||
public class Solution {
|
||
public ListNode FindKthToTail(ListNode head,int k) {
|
||
ListNode pre=null,p=null;
|
||
//两个指针都指向头结点
|
||
p=head;
|
||
pre=head;
|
||
//记录k值
|
||
int a=k;
|
||
//记录节点的个数
|
||
int count=0;
|
||
//p指针先跑,并且记录节点数,当p指针跑了k-1个节点后,pre指针开始跑,
|
||
//当p指针跑到最后时,pre所指指针就是倒数第k个节点
|
||
while(p!=null){
|
||
p=p.next;
|
||
count++;
|
||
if(k<1){
|
||
pre=pre.next;
|
||
}
|
||
k--;
|
||
}
|
||
//如果节点个数小于所求的倒数第k个节点,则返回空
|
||
if(count<a) return null;
|
||
return pre;
|
||
|
||
}
|
||
}
|
||
```
|
||
|
||
## 反转链表
|
||
|
||
**题目描述:**
|
||
|
||
输入一个链表,反转链表后,输出链表的所有元素。
|
||
|
||
**问题分析:**
|
||
|
||
链表的很常规的一道题,这一道题思路不算难,但自己实现起来真的可能会感觉无从下手,我是参考了别人的代码。
|
||
思路就是我们根据链表的特点,前一个节点指向下一个节点的特点,把后面的节点移到前面来。
|
||
就比如下图:我们把 1 节点和 2 节点互换位置,然后再将 3 节点指向 2 节点,4 节点指向 3 节点,这样以来下面的链表就被反转了。
|
||
|
||
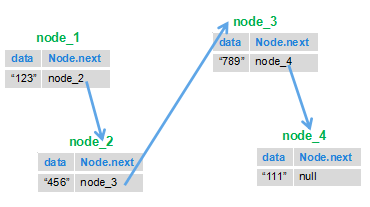
|
||
|
||
**考察内容:**
|
||
|
||
链表+代码的鲁棒性
|
||
|
||
**示例代码:**
|
||
|
||
```java
|
||
/*
|
||
public class ListNode {
|
||
int val;
|
||
ListNode next = null;
|
||
|
||
ListNode(int val) {
|
||
this.val = val;
|
||
}
|
||
}*/
|
||
public class Solution {
|
||
public ListNode ReverseList(ListNode head) {
|
||
ListNode next = null;
|
||
ListNode pre = null;
|
||
while (head != null) {
|
||
//保存要反转到头来的那个节点
|
||
next = head.next;
|
||
//要反转的那个节点指向已经反转的上一个节点
|
||
head.next = pre;
|
||
//上一个已经反转到头部的节点
|
||
pre = head;
|
||
//一直向链表尾走
|
||
head = next;
|
||
}
|
||
return pre;
|
||
}
|
||
}
|
||
```
|
||
|
||
## 合并两个排序的链表
|
||
|
||
**题目描述:**
|
||
|
||
输入两个单调递增的链表,输出两个链表合成后的链表,当然我们需要合成后的链表满足单调不减规则。
|
||
|
||
**问题分析:**
|
||
|
||
我们可以这样分析:
|
||
|
||
1. 假设我们有两个链表 A,B;
|
||
2. A 的头节点 A1 的值与 B 的头结点 B1 的值比较,假设 A1 小,则 A1 为头节点;
|
||
3. A2 再和 B1 比较,假设 B1 小,则,A1 指向 B1;
|
||
4. A2 再和 B2 比较。。。。。。。
|
||
就这样循环往复就行了,应该还算好理解。
|
||
|
||
**考察内容:**
|
||
|
||
链表+代码的鲁棒性
|
||
|
||
**示例代码:**
|
||
|
||
非递归版本:
|
||
|
||
```java
|
||
/*
|
||
public class ListNode {
|
||
int val;
|
||
ListNode next = null;
|
||
|
||
ListNode(int val) {
|
||
this.val = val;
|
||
}
|
||
}*/
|
||
public class Solution {
|
||
public ListNode Merge(ListNode list1,ListNode list2) {
|
||
//list1为空,直接返回list2
|
||
if(list1 == null){
|
||
return list2;
|
||
}
|
||
//list2为空,直接返回list1
|
||
if(list2 == null){
|
||
return list1;
|
||
}
|
||
ListNode mergeHead = null;
|
||
ListNode current = null;
|
||
//当list1和list2不为空时
|
||
while(list1!=null && list2!=null){
|
||
//取较小值作头结点
|
||
if(list1.val <= list2.val){
|
||
if(mergeHead == null){
|
||
mergeHead = current = list1;
|
||
}else{
|
||
current.next = list1;
|
||
//current节点保存list1节点的值因为下一次还要用
|
||
current = list1;
|
||
}
|
||
//list1指向下一个节点
|
||
list1 = list1.next;
|
||
}else{
|
||
if(mergeHead == null){
|
||
mergeHead = current = list2;
|
||
}else{
|
||
current.next = list2;
|
||
//current节点保存list2节点的值因为下一次还要用
|
||
current = list2;
|
||
}
|
||
//list2指向下一个节点
|
||
list2 = list2.next;
|
||
}
|
||
}
|
||
if(list1 == null){
|
||
current.next = list2;
|
||
}else{
|
||
current.next = list1;
|
||
}
|
||
return mergeHead;
|
||
}
|
||
}
|
||
```
|
||
|
||
递归版本:
|
||
|
||
```java
|
||
public ListNode Merge(ListNode list1,ListNode list2) {
|
||
if(list1 == null){
|
||
return list2;
|
||
}
|
||
if(list2 == null){
|
||
return list1;
|
||
}
|
||
if(list1.val <= list2.val){
|
||
list1.next = Merge(list1.next, list2);
|
||
return list1;
|
||
}else{
|
||
list2.next = Merge(list1, list2.next);
|
||
return list2;
|
||
}
|
||
}
|
||
```
|
||
|
||
## 用两个栈实现队列
|
||
|
||
**题目描述:**
|
||
|
||
用两个栈来实现一个队列,完成队列的 Push 和 Pop 操作。 队列中的元素为 int 类型。
|
||
|
||
**问题分析:**
|
||
|
||
先来回顾一下栈和队列的基本特点:
|
||
**栈:**后进先出(LIFO)
|
||
**队列:** 先进先出
|
||
很明显我们需要根据 JDK 给我们提供的栈的一些基本方法来实现。先来看一下 Stack 类的一些基本方法:
|
||
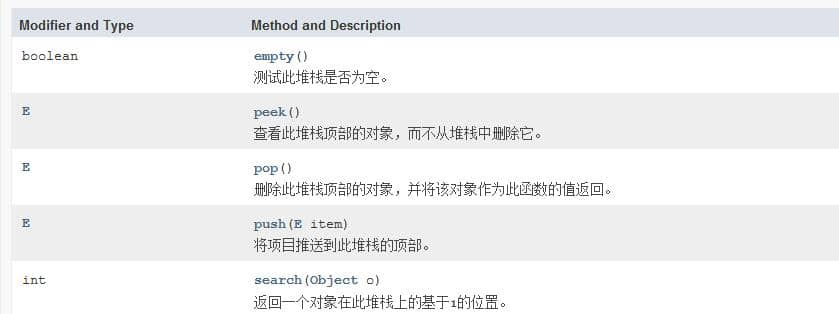
|
||
|
||
既然题目给了我们两个栈,我们可以这样考虑当 push 的时候将元素 push 进 stack1,pop 的时候我们先把 stack1 的元素 pop 到 stack2,然后再对 stack2 执行 pop 操作,这样就可以保证是先进先出的。(负[pop]负[pop]得正[先进先出])
|
||
|
||
**考察内容:**
|
||
|
||
队列+栈
|
||
|
||
示例代码:
|
||
|
||
```java
|
||
//左程云的《程序员代码面试指南》的答案
|
||
import java.util.Stack;
|
||
|
||
public class Solution {
|
||
Stack<Integer> stack1 = new Stack<Integer>();
|
||
Stack<Integer> stack2 = new Stack<Integer>();
|
||
|
||
//当执行push操作时,将元素添加到stack1
|
||
public void push(int node) {
|
||
stack1.push(node);
|
||
}
|
||
|
||
public int pop() {
|
||
//如果两个队列都为空则抛出异常,说明用户没有push进任何元素
|
||
if(stack1.empty()&&stack2.empty()){
|
||
throw new RuntimeException("Queue is empty!");
|
||
}
|
||
//如果stack2不为空直接对stack2执行pop操作,
|
||
if(stack2.empty()){
|
||
while(!stack1.empty()){
|
||
//将stack1的元素按后进先出push进stack2里面
|
||
stack2.push(stack1.pop());
|
||
}
|
||
}
|
||
return stack2.pop();
|
||
}
|
||
}
|
||
```
|
||
|
||
## 栈的压入,弹出序列
|
||
|
||
**题目描述:**
|
||
|
||
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列 1,2,3,4,5 是某栈的压入顺序,序列 4,5,3,2,1 是该压栈序列对应的一个弹出序列,但 4,3,5,1,2 就不可能是该压栈序列的弹出序列。(注意:这两个序列的长度是相等的)
|
||
|
||
**题目分析:**
|
||
|
||
这道题想了半天没有思路,参考了 Alias 的答案,他的思路写的也很详细应该很容易看懂。
|
||
作者:Alias
|
||
https://www.nowcoder.com/questionTerminal/d77d11405cc7470d82554cb392585106
|
||
来源:牛客网
|
||
|
||
【思路】借用一个辅助的栈,遍历压栈顺序,先讲第一个放入栈中,这里是 1,然后判断栈顶元素是不是出栈顺序的第一个元素,这里是 4,很显然 1≠4,所以我们继续压栈,直到相等以后开始出栈,出栈一个元素,则将出栈顺序向后移动一位,直到不相等,这样循环等压栈顺序遍历完成,如果辅助栈还不为空,说明弹出序列不是该栈的弹出顺序。
|
||
|
||
举例:
|
||
|
||
入栈 1,2,3,4,5
|
||
|
||
出栈 4,5,3,2,1
|
||
|
||
首先 1 入辅助栈,此时栈顶 1≠4,继续入栈 2
|
||
|
||
此时栈顶 2≠4,继续入栈 3
|
||
|
||
此时栈顶 3≠4,继续入栈 4
|
||
|
||
此时栈顶 4 = 4,出栈 4,弹出序列向后一位,此时为 5,,辅助栈里面是 1,2,3
|
||
|
||
此时栈顶 3≠5,继续入栈 5
|
||
|
||
此时栈顶 5=5,出栈 5,弹出序列向后一位,此时为 3,,辅助栈里面是 1,2,3
|
||
|
||
….
|
||
依次执行,最后辅助栈为空。如果不为空说明弹出序列不是该栈的弹出顺序。
|
||
|
||
**考察内容:**
|
||
|
||
栈
|
||
|
||
**示例代码:**
|
||
|
||
```java
|
||
import java.util.ArrayList;
|
||
import java.util.Stack;
|
||
//这道题没想出来,参考了Alias同学的答案:https://www.nowcoder.com/questionTerminal/d77d11405cc7470d82554cb392585106
|
||
public class Solution {
|
||
public boolean IsPopOrder(int [] pushA,int [] popA) {
|
||
if(pushA.length == 0 || popA.length == 0)
|
||
return false;
|
||
Stack<Integer> s = new Stack<Integer>();
|
||
//用于标识弹出序列的位置
|
||
int popIndex = 0;
|
||
for(int i = 0; i< pushA.length;i++){
|
||
s.push(pushA[i]);
|
||
//如果栈不为空,且栈顶元素等于弹出序列
|
||
while(!s.empty() &&s.peek() == popA[popIndex]){
|
||
//出栈
|
||
s.pop();
|
||
//弹出序列向后一位
|
||
popIndex++;
|
||
}
|
||
}
|
||
return s.empty();
|
||
}
|
||
}
|
||
```
|
||
|
||
<!-- @include: @article-footer.snippet.md --> |