fix redis.md bug

README.md

@@ -1,16 +1,16 @@
-如果你不知道该学习什么的话，请看 [Java 学习线路图是怎样的？]( https://www.zhihu.com/question/56110328/answer/869069586)  （原创不易，欢迎点赞），这是 2021 最新最完善的 Java 学习路线！
+👉 如果你不知道该学习什么的话，请看 [Java 学习线路图是怎样的？]( https://zhuanlan.zhihu.com/p/379041500)  （原创不易，欢迎点赞），这是 2021 最新最完善的 Java 学习路线！另外，[我的朋友整理了一份消息队列常见面试题，需要的小伙伴可以点击领取！](http://mp.weixin.qq.com/s?__biz=Mzg2OTA0Njk0OA==&mid=100025985&idx=1&sn=681af486050fabbeea27fa1c3bec5d65&chksm=4ea1e94a79d6605c72f280b5268100c6e96c6ab1dc9a0178b33e25a72ff5f4eac3dcb56fa44f#rd)
 
-👍推荐 [在线阅读](https://snailclimb.gitee.io/javaguide)  (Github 访问速度比较慢可能会导致部分图片无法刷新出来) 
+👉 推荐 [在线阅读](https://snailclimb.gitee.io/javaguide)  (Github 访问速度比较慢可能会导致部分图片无法刷新出来) 
 
-👍推荐[2021最新实战项目源码下载](https://mp.weixin.qq.com/s?__biz=Mzg2OTA0Njk0OA==&mid=100018862&idx=1&sn=858e00b60c6097e3ba061e79be472280&chksm=4ea1856579d60c73224e4d852af6b0188c3ab905069fc28f4b293963fd1ee55d2069fb229848#rd)
-
-书单已经被移动到[awesome-cs](https://github.com/CodingDocs/awesome-cs) 这个仓库。
+👉 书单已经被移动到 [awesome-cs](https://github.com/CodingDocs/awesome-cs) 这个仓库。
 
 > 1. **介绍**：关于 JavaGuide 的相关介绍请看：[关于 JavaGuide 的一些说明](https://www.yuque.com/snailclimb/dr6cvl/mr44yt) 。
-> 2. **PDF版本** ： [《JavaGuide 面试突击版》PDF 版本](#公众号) 。[图解计算机基础 PDF 版](#优质原创PDF资源)。
-> 3. **知识星球** :  简历指导/Java学习/面试指导/面试小册。欢迎加入[我的知识星球](https://mp.weixin.qq.com/s?__biz=Mzg2OTA0Njk0OA==&mid=100015911&idx=1&sn=2e8a0f5acb749ecbcbb417aa8a4e18cc&chksm=4ea1b0ec79d639fae37df1b86f196e8ce397accfd1dd2004bcadb66b4df5f582d90ae0d62448#rd) 。星球内部更新的[《Java面试进阶指北  打造个人的技术竞争力》](https://www.yuque.com/docs/share/f37fc804-bfe6-4b0d-b373-9c462188fec7)这个小册的质量很高，专为面试打造。
-> 4. **面试专版** ：准备面试的小伙伴可以考虑面试专版：[《Java 面试进阶指南》](https://xiaozhuanlan.com/javainterview?rel=javaguide) 
-> 6. **转载须知** ：以下所有文章如非文首说明皆为我（Guide哥）的原创，转载在文首注明出处，如发现恶意抄袭/搬运，会动用法律武器维护自己的权益。让我们一起维护一个良好的技术创作环境！⛽️
+> 2. **贡献指南** ：欢迎参与 [JavaGuide的维护工作](https://github.com/Snailclimb/JavaGuide/issues/1235)，这是一件非常有意义的事情。
+> 3. **PDF版本** ： [《JavaGuide 面试突击版》PDF 版本](#公众号) 。
+> 4. **图解计算机基础** ：[图解计算机基础 PDF 下载](https://mp.weixin.qq.com/s?__biz=Mzg2OTA0Njk0OA==&mid=100021725&idx=1&sn=2db9664ca25363139a81691043e9fd8f&chksm=4ea19a1679d61300d8990f7e43bfc7f476577a81b712cf0f9c6f6552a8b219bc081efddb5c54#rd) 。
+> 5. **知识星球** :  简历指导/Java学习/面试指导/面试小册。欢迎加入[我的知识星球](https://mp.weixin.qq.com/s?__biz=Mzg2OTA0Njk0OA==&mid=100015911&idx=1&sn=2e8a0f5acb749ecbcbb417aa8a4e18cc&chksm=4ea1b0ec79d639fae37df1b86f196e8ce397accfd1dd2004bcadb66b4df5f582d90ae0d62448#rd) 。
+> 6. **面试专版** ：准备面试的小伙伴可以考虑面试专版：[《Java面试进阶指北 》](https://www.yuque.com/docs/share/f37fc804-bfe6-4b0d-b373-9c462188fec7) (质量很高，专为面试打造)
+> 7. **转载须知** ：以下所有文章如非文首说明皆为我（Guide哥）的原创，转载在文首注明出处，如发现恶意抄袭/搬运，会动用法律武器维护自己的权益。让我们一起维护一个良好的技术创作环境！⛽️
 
 <p align="center">
 <a href="https://github.com/Snailclimb/JavaGuide" target="_blank">
@@ -44,10 +44,10 @@
 
 ### 基础
 
-**知识点/面试题:**(必看:+1: )
+**知识点/面试题** : (必看:+1: )
 
 1. **[Java 基础知识](docs/java/basis/Java基础知识.md)**
-2. **[Java 基础知识疑难点/易错点](docs/java/basis/Java基础知识疑难点.md)**
+2. [Java 基础知识疑难点/易错点](docs/java/basis/Java基础知识疑难点.md)
 
 **重要知识点详解：**
 
@@ -61,6 +61,7 @@
 
 1. **[Java 容器常见问题总结](docs/java/collection/Java集合框架常见面试题.md)** (必看 :+1:)
 2. **源码分析** ：[ArrayList 源码+扩容机制分析](docs/java/collection/ArrayList源码+扩容机制分析.md) 、[LinkedList 源码](docs/java/collection/LinkedList源码分析.md) 、[HashMap(JDK1.8)源码+底层数据结构分析](<docs/java/collection/HashMap(JDK1.8)源码+底层数据结构分析.md>) 、[ConcurrentHashMap 源码+底层数据结构分析](docs/java/collection/ConcurrentHashMap源码+底层数据结构分析.md)
+3. [Java 容器使用注意事项总结](docs/java/collection/Java集合使用注意事项总结.md)
 
 ### 并发
 
@@ -71,14 +72,17 @@
 
 **重要知识点详解：**
 
-2. **线程池**：[Java 线程池学习总结](./docs/java/multi-thread/java线程池学习总结.md)、[拿来即用的线程池最佳实践](./docs/java/multi-thread/拿来即用的线程池最佳实践.md)
-4. [ ThreadLocal 关键字解析](docs/java/multi-thread/万字详解ThreadLocal关键字.md)
-5. [并发容器总结](docs/java/multi-thread/并发容器总结.md)
-6. [JUC 中的 Atomic 原子类总结](docs/java/multi-thread/Atomic原子类总结.md)
-7. [AQS 原理以及 AQS 同步组件总结](docs/java/multi-thread/AQS原理以及AQS同步组件总结.md)
+1. **线程池**：[Java 线程池学习总结](./docs/java/multi-thread/java线程池学习总结.md)、[拿来即用的线程池最佳实践](./docs/java/multi-thread/拿来即用的线程池最佳实践.md)
+2. [ ThreadLocal 关键字解析](docs/java/multi-thread/万字详解ThreadLocal关键字.md)
+3. [并发容器总结](docs/java/multi-thread/并发容器总结.md)
+4. [JUC 中的 Atomic 原子类总结](docs/java/multi-thread/Atomic原子类总结.md)
+5. [AQS 原理以及 AQS 同步组件总结](docs/java/multi-thread/AQS原理以及AQS同步组件总结.md)
+6. [CompletableFuture入门](docs/java/multi-thread/CompletableFuture入门.md)
 
 ### JVM (必看 :+1:)
 
+JVM 这部分内容主要参考 [JVM 虚拟机规范-Java8 ](https://docs.oracle.com/javase/specs/jvms/se8/html/index.html) 和周志明老师的[《深入理解Java虚拟机（第3版）》](https://book.douban.com/subject/34907497/) （强烈建议阅读多遍！）。
+
 1. **[Java 内存区域](docs/java/jvm/Java内存区域.md)**
 2. **[JVM 垃圾回收](docs/java/jvm/JVM垃圾回收.md)**
 3. [JDK 监控和故障处理工具](docs/java/jvm/JDK监控和故障处理工具总结.md)
@@ -91,27 +95,40 @@
 ### 新特性
 
 1.  **Java 8** ：[Java 8 新特性总结](docs/java/new-features/Java8新特性总结.md)、[Java8常用新特性总结](docs/java/new-features/java8-common-new-features.md) 、[Java 8 学习资源推荐](docs/java/new-features/Java8教程推荐.md)、[Java8 forEach 指南](docs/java/new-features/Java8foreach指南.md)
-2.  **Java9~Java14** : [一文带你看遍 JDK9~14 的重要新特性！](./docs/java/new-features/一文带你看遍JDK9到14的重要新特性.md)
+2.  **Java9~Java15** : [一文带你看遍 JDK9~15 的重要新特性！](./docs/java/new-features/java新特性总结.md)
 
-## 网络
+### 小技巧
 
-1. [计算机网络常见面试题](docs/network/计算机网络.md)
-2. [计算机网络基础知识总结](docs/network/计算机网络知识总结.md)
+1. [JAD 反编译](docs/java/tips/JAD反编译tricks.md)
+2. [手把手教你定位常见 Java 性能问题](./docs/java/tips/手把手教你定位常见Java性能问题.md)
 
-## 操作系统
+## 计算机基础
 
-1. [操作系统常见问题总结！](docs/operating-system/basis.md)
-2. [后端程序员必备的 Linux 基础知识](docs/operating-system/linux.md)
-3. [Shell 编程入门](docs/operating-system/Shell.md)
+👉 **[图解计算机基础 PDF 下载](https://mp.weixin.qq.com/s?__biz=Mzg2OTA0Njk0OA==&mid=100021725&idx=1&sn=2db9664ca25363139a81691043e9fd8f&chksm=4ea19a1679d61300d8990f7e43bfc7f476577a81b712cf0f9c6f6552a8b219bc081efddb5c54#rd)** 。
 
-## 数据结构与算法
+### 操作系统
+
+1. [操作系统常见问题总结！](docs/cs-basics/operating-system/basis.md)
+2. [后端程序员必备的 Linux 基础知识总结](docs/cs-basics/operating-system/linux.md)
+3. [Shell 编程入门](docs/cs-basics/operating-system/Shell.md)
+
+### 网络
+
+1. [计算机网络常见面试题](docs/cs-basics/network/计算机网络.md)
+2. [计算机网络基础知识总结](docs/cs-basics/network/计算机网络知识总结.md)
 
 ### 数据结构
 
-- **图解数据结构：**
-  1. [线性数据结构 :数组、链表、栈、队列](docs/dataStructures-algorithms/data-structure/线性数据结构.md)
-  2. [图](docs/dataStructures-algorithms/data-structure/图.md)
-- [不了解布隆过滤器？一文给你整的明明白白！](docs/dataStructures-algorithms/data-structure/bloom-filter.md)
+**图解数据结构：**
+
+1. [线性数据结构 :数组、链表、栈、队列](docs/cs-basics/data-structure/线性数据结构.md)
+2. [图](docs/cs-basics/data-structure/图.md)
+3. [堆](docs/cs-basics/data-structure/堆.md)
+4. [树](docs/cs-basics/data-structure/树.md) ：重点关注[红黑树](docs/cs-basics/data-structure/红黑树.md)、B-，B+，B*树、LSM树
+
+其他常用数据结构 ：
+
+1. [布隆过滤器](docs/cs-basics/data-structure/bloom-filter.md)
 
 ### 算法
 
@@ -120,11 +137,13 @@
 - [算法学习书籍+资源推荐](https://www.zhihu.com/question/323359308/answer/1545320858) 。
 - [如何刷Leetcode?](https://www.zhihu.com/question/31092580/answer/1534887374) 
 
-**常见算法问题总结：**
+**常见算法问题总结** ：
 
-- [几道常见的字符串算法题总结 ](docs/dataStructures-algorithms/几道常见的子符串算法题.md)
-- [几道常见的链表算法题总结 ](docs/dataStructures-algorithms/几道常见的链表算法题.md)
-- [剑指 offer 部分编程题](docs/dataStructures-algorithms/剑指offer部分编程题.md)
+- [几道常见的字符串算法题总结 ](docs/cs-basics/algorithms/几道常见的字符串算法题.md)
+- [几道常见的链表算法题总结 ](docs/cs-basics/algorithms/几道常见的链表算法题.md)
+- [剑指 offer 部分编程题](docs/cs-basics/algorithms/剑指offer部分编程题.md)
+
+另外，[GeeksforGeeks]( https://www.geeksforgeeks.org/fundamentals-of-algorithms/) 这个网站总结了常见的算法 ，比较全面系统。
 
 ## 数据库
 
@@ -132,23 +151,30 @@
 
 **总结：**
 
-1. **[MySQL知识点总结](docs/database/MySQL.md)** (必看 :+1:)
-2. [阿里巴巴开发手册数据库部分的一些最佳实践](docs/database/阿里巴巴开发手册数据库部分的一些最佳实践.md)
-3. [一千行 MySQL 学习笔记](docs/database/一千行MySQL命令.md)
-4. [MySQL 高性能优化规范建议](docs/database/MySQL高性能优化规范建议.md)
+1. [数据库基础知识总结](docs/database/数据库基础知识.md)
+2. **[MySQL知识点总结](docs/database/mysql/MySQL总结.md)** (必看 :+1:)
+3. [阿里巴巴开发手册数据库部分的一些最佳实践](docs/database/mysql/阿里巴巴开发手册数据库部分的一些最佳实践.md)
+4. [一千行 MySQL 学习笔记](docs/database/mysql/一千行MySQL学习笔记.md)
+5. [MySQL 高性能优化规范建议](docs/database/mysql/MySQL高性能优化规范建议.md)
 
 **重要知识点：**
 
-1. [MySQL数据库索引总结](docs/database/MySQL数据库索引.md)
-2. [事务隔离级别(图文详解)](<docs/database/事务隔离级别(图文详解).md>)
-3. [一条 SQL 语句在 MySQL 中如何执行的](docs/database/一条sql语句在mysql中如何执行的.md)
-4. [关于数据库中如何存储时间的一点思考](docs/database/关于数据库存储时间的一点思考.md)
+1. [MySQL数据库索引总结](docs/database/mysql/MySQL数据库索引.md)
+2. [事务隔离级别(图文详解)](docs/database/mysql/事务隔离级别(图文详解).md)
+3. [MySQL三大日志(binlog、redo log和undo log)详解](docs/database/mysql/MySQL三大日志.md)
+4. [InnoDB存储引擎对MVCC的实现](docs/database/mysql/InnoDB对MVCC的实现.md)
+5. [一条 SQL 语句在 MySQL 中如何执行的](docs/database/mysql/一条sql语句在mysql中如何执行的.md)
+6. [关于数据库中如何存储时间的一点思考](docs/database/mysql/关于数据库存储时间的一点思考.md)
 
 ### Redis
 
 2. [Redis 常见问题总结](docs/database/Redis/redis-all.md)
 3. [面试/工作必备！3种常用的缓存读写策略！](docs/database/Redis/3种常用的缓存读写策略.md)
 
+## 搜索引擎
+
+用于提高搜索效率，功能和浏览器搜索引擎类似。比较常见的搜索引擎是 Elasticsearch（推荐） 和 Solr。
+
 ## 系统设计
 
 ### 系统设计必备基础
@@ -234,10 +260,6 @@ CAP 也就是 Consistency（一致性）、Availability（可用性）、Partiti
 
 **Paxos 算法**诞生于 1990 年，这是一种解决分布式系统一致性的经典算法 。但是，由于 Paxos 算法非常难以理解和实现，不断有人尝试简化这一算法。到了2013 年才诞生了一个比 Paxos 算法更易理解和实现的分布式一致性算法—**Raft 算法**。
 
-#### 搜索引擎
-
-用于提高搜索效率，功能和浏览器搜索引擎类似。比较常见的搜索引擎是 Elasticsearch（推荐） 和 Solr。
-
 #### RPC
 
 RPC 让调用远程服务调用像调用本地方法那样简单。
@@ -256,7 +278,7 @@ Dubbo 是一款国产的 RPC 框架，由阿里开源。相关阅读：
 
 #### 分布式 id
 
-在复杂分布式系统中，往往需要对大量的数据和消息进行唯一标识。比如数据量太大之后，往往需要对进行对数据进行分库分表，分库分表后需要有一个唯一 ID 来标识一条数据或消息，数据库的自增 ID 显然不能满足需求。相关阅读：[为什么要分布式 id ？分布式 id 生成方案有哪些？](docs/system-design/micro-service/分布式id生成方案总结.md)
+在复杂分布式系统中，往往需要对大量的数据和消息进行唯一标识。比如数据量太大之后，往往需要对数据进行分库分表，分库分表后需要有一个唯一 ID 来标识一条数据或消息，数据库的自增 ID 显然不能满足需求。相关阅读：[为什么要分布式 id ？分布式 id 生成方案有哪些？](docs/system-design/micro-service/分布式id生成方案总结.md)
 
 #### 分布式事务
 
@@ -339,6 +361,24 @@ Dubbo 是一款国产的 RPC 框架，由阿里开源。相关阅读：
 
 另外，重试的次数一般设为 3 次，再多次的重试没有好处，反而会加重服务器压力（部分场景使用失败重试机制会不太适合）。
 
+#### 灾备设计
+
+**灾备**  = 容灾+备份。
+
+- **备份** ： 将系统所产生的的所有重要数据多备份几份。
+- **容灾** ： 在异地建立两个完全相同的系统。当某个地方的系统突然挂掉，整个应用系统可以切换到另一个，这样系统就可以正常提供服务了。
+
+#### 异地多活
+
+异地多活描述的是将服务部署在异地并且服务同时对外提供服务。和传统的灾备设计的最主要区别在于“多活”，即所有站点都是同时在对外提供服务的。
+
+异地多活是为了应对突发状况比如火灾、地震等自然或者认为灾害。
+
+相关阅读：
+
+- [四步构建异地多活](https://mp.weixin.qq.com/s/hMD-IS__4JE5_nQhYPYSTg)
+- [《从零开始学架构》— 28 | 业务高可用的保障：异地多活架构](http://gk.link/a/10pKZ)
+
 ### 大型网站架构
 
 - [8 张图读懂大型网站技术架构](docs/system-design/website-architecture/8%20张图读懂大型网站技术架构.md)
@@ -346,7 +386,6 @@ Dubbo 是一款国产的 RPC 框架，由阿里开源。相关阅读：
 
 ## 工具
 
-1. **Java** ：[JAD 反编译](docs/java/JAD反编译tricks.md)、[手把手教你定位常见 Java 性能问题](./docs/java/手把手教你定位常见Java性能问题.md)
 2. **Git** ：[Git 入门](docs/tools/Git.md)
 3. **Github** ： [Github小技巧](docs/tools/Github技巧.md)
 4. **Docker** : [Docker 基本概念解读](docs/tools/Docker.md) 、[Docker从入门到上手干事](docs/tools/Docker从入门到实战.md)
@@ -370,15 +409,8 @@ Dubbo 是一款国产的 RPC 框架，由阿里开源。相关阅读：
 
 ### 待办
 
-- [ ] 数据结构总结重构
-
-### 优质原创PDF资源
-
-![](https://cdn.jsdelivr.net/gh/javaguide-tech/blog-images-2@main/%E8%AE%A1%E7%AE%97%E6%9C%BA%E4%B8%93%E4%B8%9A/image-20201027160348395.png)
-
-为了避免恶意传播，微信搜“**Github掘金计划**”后台回复 **“006”** 即可获取。
-
-<img src="https://cdn.jsdelivr.net/gh/javaguide-tech/blog-images-2@main/%E7%B3%BB%E7%BB%9F%E8%AE%BE%E8%AE%A1/qrcode_for_gh_8b9b6034ac19_258.jpg" style="text-align:right"/>
+- [ ] 计算机网络知识点完善
+- [ ] 分布式常见理论和算法总结完善
 
 ### 捐赠支持
 
@@ -388,7 +420,11 @@ Dubbo 是一款国产的 RPC 框架，由阿里开源。相关阅读：
 
 ### 联系我
 
-<img src="https://cdn.jsdelivr.net/gh/javaguide-tech/blog-images-3@main/%E8%AF%BB%E4%B9%A6%E7%AC%94%E8%AE%B0/31603935587_.pic_hd.jpg" style="zoom:67%;" />
+![各种技术的学习路线](https://img-blog.csdnimg.cn/20210609102613344.png)
+
+整理了一份各个技术的学习路线，需要的小伙伴加我微信：“**JavaGuide1996**”备注“**Github-学习路线**”即可！
+
+![](https://img-blog.csdnimg.cn/20210609084555810.jpg)
 
 ### 公众号
 
@@ -397,4 +433,3 @@ Dubbo 是一款国产的 RPC 框架，由阿里开源。相关阅读：
 **《Java 面试突击》:** 由本文档衍生的专为面试而生的《Java 面试突击》V4.0 PDF 版本[公众号](#公众号)后台回复 **"面试突击"** 即可领取！
 
 ![我的公众号](https://cdn.jsdelivr.net/gh/javaguide-tech/blog-images/2020-08/167598cd2e17b8ec.png)
-

docs/cs-basics/algorithms/几道常见的链表算法题.md

@@ -50,7 +50,7 @@ Leetcode官方详细解答地址：
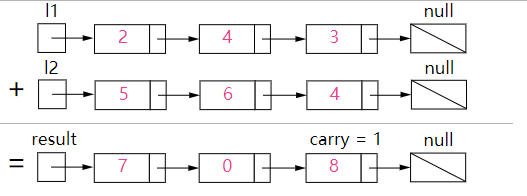
 我们使用变量来跟踪进位，并从包含最低有效位的表头开始模拟逐
 位相加的过程。
 
-![图1，对两数相加方法的可视化: 342 + 465 = 807342+465=807， 每个结点都包含一个数字，并且数字按位逆序存储。](http://my-blog-to-use.oss-cn-beijing.aliyuncs.com/18-9-20/34910956.jpg)
+![图1，对两数相加方法的可视化: 342 + 465 = 807342+465=807， 每个结点都包含一个数字，并且数字按位逆序存储。](https://my-blog-to-use.oss-cn-beijing.aliyuncs.com/18-9-20/34910956.jpg)
 
 ### Solution
 
@@ -98,7 +98,7 @@ public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
 ### 题目描述
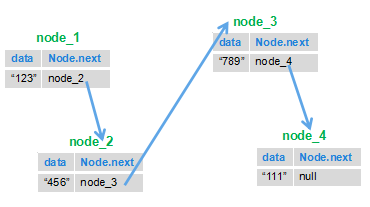
 > 剑指 offer:输入一个链表，反转链表后，输出链表的所有元素。
 
-![翻转链表](http://my-blog-to-use.oss-cn-beijing.aliyuncs.com/18-9-20/81431871.jpg)
+![翻转链表](https://my-blog-to-use.oss-cn-beijing.aliyuncs.com/18-9-20/81431871.jpg)
 
 ### 问题分析
 
@@ -269,7 +269,7 @@ public class Solution {
 
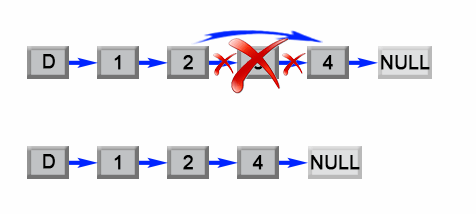
 我们注意到这个问题可以容易地简化成另一个问题：删除从列表开头数起的第 (L - n + 1)个结点，其中 L是列表的长度。只要我们找到列表的长度 L，这个问题就很容易解决。
 
-![图 1. 删除列表中的第 L - n + 1 个元素](http://my-blog-to-use.oss-cn-beijing.aliyuncs.com/18-9-20/94354387.jpg)
+![图 1. 删除列表中的第 L - n + 1 个元素](https://my-blog-to-use.oss-cn-beijing.aliyuncs.com/18-9-20/94354387.jpg)
 
 ### Solution
 

docs/cs-basics/algorithms/剑指offer部分编程题.md

@@ -14,38 +14,36 @@ n<=39
 **采用迭代法：**
 
 ```java
-  int Fibonacci(int number) {
-			if (number <= 0) {
-				return 0;
-			}
-			if (number == 1 || number == 2) {
-				return 1;
-			}
-			int first = 1, second = 1, third = 0;
-			for (int i = 3; i <= number; i++) {
-				third = first + second;
-				first = second;
-				second = third;
-			}
-			return third;
-		}
+int Fibonacci(int number) {
+    if (number <= 0) {
+        return 0;
+    }
+    if (number == 1 || number == 2) {
+        return 1;
+    }
+    int first = 1, second = 1, third = 0;
+    for (int i = 3; i <= number; i++) {
+        third = first + second;
+        first = second;
+        second = third;
+    }
+    return third;
+}
 ```
 
 **采用递归：**
 
 ```java
-		 public int Fibonacci(int n) {
-           
-			if (n <= 0) {
-				return 0;
-			}
-			if (n == 1||n==2) {
-				return 1;
-			}
+public int Fibonacci(int n) {
+    if (n <= 0) {
+        return 0;
+    }
+    if (n == 1||n==2) {
+        return 1;
+    }
 
-			return Fibonacci(n - 2) + Fibonacci(n - 1);
-
-		}
+    return Fibonacci(n - 2) + Fibonacci(n - 1);
+}
 ```
 
 ### 二 跳台阶问题
@@ -71,24 +69,24 @@ f(1) = 1, f(2) = 2, f(3) = 3, f(4) = 5，  可以总结出f(n) = f(n-1) + f(n-2)
 #### **示例代码：**
 
 ```java
-	int jumpFloor(int number) {
-			if (number <= 0) {
-				return 0;
-			}
-			if (number == 1) {
-				return 1;
-			}
-			if (number == 2) {
-				return 2;
-			}
-			int first = 1, second = 2, third = 0;
-			for (int i = 3; i <= number; i++) {
-				third = first + second;
-				first = second;
-				second = third;
-			}
-			return third;
-		}
+int jumpFloor(int number) {
+    if (number <= 0) {
+        return 0;
+    }
+    if (number == 1) {
+        return 1;
+    }
+    if (number == 2) {
+        return 2;
+    }
+    int first = 1, second = 2, third = 0;
+    for (int i = 3; i <= number; i++) {
+        third = first + second;
+        first = second;
+        second = third;
+    }
+    return third;
+}
 ```
 
 ### 三 变态跳台阶问题
@@ -113,9 +111,9 @@ f(n)=f(n-1)+f(n-2)+...+f(1)
 #### **示例代码：**
 
 ```java
-     int JumpFloorII(int number) {
-		return 1 << --number;//2^(number-1)用位移操作进行，更快
-	}
+int JumpFloorII(int number) {
+    return 1 << --number;//2^(number-1)用位移操作进行，更快
+}
 ```
 
 #### **补充：**
@@ -124,7 +122,7 @@ f(n)=f(n-1)+f(n-2)+...+f(1)
 
 1. “<<” :     **左移运算符**，等同于乘2的n次方
 2. “>>”:     **右移运算符**，等同于除2的n次方
-3. “>>>” **无符号右移运算符**，不管移动前最高位是0还是1，右移后左侧产生的空位部分都以0来填充。与>>类似。
+3. “>>>” :  **无符号右移运算符**，不管移动前最高位是0还是1，右移后左侧产生的空位部分都以0来填充。与>>类似。
    例：
     int a = 16;
     int b = a << 2;//左移2，等同于16 * 2的2次方，也就是16 * 4
@@ -147,22 +145,22 @@ f(n)=f(n-1)+f(n-2)+...+f(1)
 #### **示例代码：**
 
 ```java
-    public boolean Find(int target, int [][] array) {
-        //基本思路从左下角开始找，这样速度最快
-       int row = array.length-1;//行
-        int column = 0;//列
-        //当行数大于0，当前列数小于总列数时循环条件成立
-        while((row >= 0)&& (column< array[0].length)){
-            if(array[row][column] > target){
-                row--;
-            }else if(array[row][column] < target){
-               column++;
-            }else{
-                return true;
-            }
+public boolean Find(int target, int [][] array) {
+    //基本思路从左下角开始找，这样速度最快
+    int row = array.length-1;//行
+    int column = 0;//列
+    //当行数大于0，当前列数小于总列数时循环条件成立
+    while((row >= 0)&& (column< array[0].length)){
+        if(array[row][column] > target){
+            row--;
+        }else if(array[row][column] < target){
+            column++;
+        }else{
+            return true;
         }
-        return false;
     }
+    return false;
+}
 ```
 
 ### 五 替换空格
@@ -175,38 +173,37 @@ f(n)=f(n-1)+f(n-2)+...+f(1)
 
 这道题不难，我们可以通过循环判断字符串的字符是否为空格，是的话就利用append()方法添加追加“%20”，否则还是追加原字符。
 
-或者最简单的方法就是利用： replaceAll(String regex,String replacement)方法了，一行代码就可以解决。
+或者最简单的方法就是利用：replaceAll(String regex,String replacement)方法了，一行代码就可以解决。
 
 #### **示例代码：**
 
 **常规做法：**
 
 ```java
-    public String replaceSpace(StringBuffer str) {
-        StringBuffer out=new StringBuffer();
-        for (int i = 0; i < str.toString().length(); i++) {
-            char b=str.charAt(i);
-            if(String.valueOf(b).equals(" ")){
-                out.append("%20");
-            }else{
-                out.append(b);
-            }
+public String replaceSpace(StringBuffer str) {
+    StringBuffer out = new StringBuffer();
+    for (int i = 0; i < str.toString().length(); i++) {
+        char b = str.charAt(i);
+        if(String.valueOf(b).equals(" ")){
+            out.append("%20");
+        }else{
+            out.append(b);
         }
-        return out.toString();     
     }
+    return out.toString();     
+}
 ```
 
 **一行代码解决：**
 
 ```java
-    public String replaceSpace(StringBuffer str) {
-        //return str.toString().replaceAll(" ", "%20");
-        //public String replaceAll(String regex,String replacement)
-        //用给定的替换替换与给定的regular expression匹配的此字符串的每个子字符串。 
-        //\ 转义字符. 如果你要使用 "\" 本身, 则应该使用 "\\". String类型中的空格用“\s”表示，所以我这里猜测"\\s"就是代表空格的意思
-        return str.toString().replaceAll("\\s", "%20");
-    }
-
+public String replaceSpace(StringBuffer str) {
+    //return str.toString().replaceAll(" ", "%20");
+    //public String replaceAll(String regex,String replacement)
+    //用给定的替换替换与给定的regular expression匹配的此字符串的每个子字符串。 
+    //\ 转义字符. 如果你要使用 "\" 本身, 则应该使用 "\\". String类型中的空格用“\s”表示，所以我这里猜测"\\s"就是代表空格的意思
+    return str.toString().replaceAll("\\s", "%20");
+}
 ```
 
 ### 六 数值的整数次方
@@ -279,17 +276,17 @@ public class Solution {
 当然这一题也可以采用笨方法：累乘。不过这种方法的时间复杂度为O（n），这样没有前一种方法效率高。
 
 ```java
-    // 使用累乘
-    public double powerAnother(double base, int exponent) {
-        double result = 1.0;
-        for (int i = 0; i < Math.abs(exponent); i++) {
-            result *= base;
-        }
-        if (exponent >= 0)
-            return result;
-        else
-            return 1 / result;
+// 使用累乘
+public double powerAnother(double base, int exponent) {
+    double result = 1.0;
+    for (int i = 0; i < Math.abs(exponent); i++) {
+        result *= base;
     }
+    if (exponent >= 0)
+        return result;
+    else
+        return 1 / result;
+}
 ```
 
 ### 七 调整数组顺序使奇数位于偶数前面
@@ -434,22 +431,21 @@ public class ListNode {
     }
 }*/
 public class Solution {
-public ListNode ReverseList(ListNode head) {
-   ListNode next = null;
-   ListNode pre = null;
-    while (head != null) {
-          //保存要反转到头来的那个节点
-           next = head.next;
-           //要反转的那个节点指向已经反转的上一个节点
-           head.next = pre;
-           //上一个已经反转到头部的节点
-           pre = head;
-           //一直向链表尾走
-           head = next;
+    public ListNode ReverseList(ListNode head) {
+       ListNode next = null;
+       ListNode pre = null;
+        while (head != null) {
+              //保存要反转到头来的那个节点
+               next = head.next;
+               //要反转的那个节点指向已经反转的上一个节点
+               head.next = pre;
+               //上一个已经反转到头部的节点
+               pre = head;
+               //一直向链表尾走
+               head = next;
+        }
+        return pre;
     }
-    return pre;
-}
-
 }
 ```
 
@@ -538,20 +534,20 @@ public class Solution {
 
 ```java
 public ListNode Merge(ListNode list1,ListNode list2) {
-       if(list1 == null){
-           return list2;
-       }
-       if(list2 == null){
-           return list1;
-       }
-       if(list1.val <= list2.val){
-           list1.next = Merge(list1.next, list2);
-           return list1;
-       }else{
-           list2.next = Merge(list1, list2.next);
-           return list2;
-       }       
-   }
+    if(list1 == null){
+        return list2;
+    }
+    if(list2 == null){
+        return list1;
+    }
+    if(list1.val <= list2.val){
+        list1.next = Merge(list1.next, list2);
+        return list1;
+    }else{
+        list2.next = Merge(list1, list2.next);
+        return list2;
+    }       
+}
 ```
 
 ### 十一 用两个栈实现队列
@@ -566,7 +562,7 @@ public ListNode Merge(ListNode list1,ListNode list2) {
 **栈：**后进先出（LIFO）
 **队列：** 先进先出
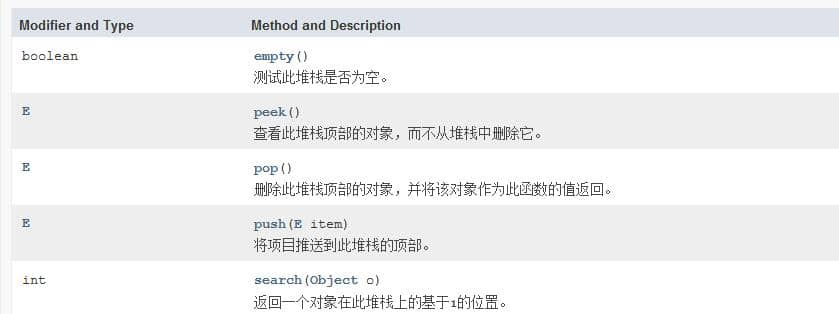
 很明显我们需要根据JDK给我们提供的栈的一些基本方法来实现。先来看一下Stack类的一些基本方法：
-![Stack类的一些常见方法](http://my-blog-to-use.oss-cn-beijing.aliyuncs.com/18-4-4/5985000.jpg)
+![Stack类的一些常见方法](https://my-blog-to-use.oss-cn-beijing.aliyuncs.com/18-4-4/5985000.jpg)
 
 既然题目给了我们两个栈，我们可以这样考虑当push的时候将元素push进stack1，pop的时候我们先把stack1的元素pop到stack2，然后再对stack2执行pop操作，这样就可以保证是先进先出的。（负[pop]负[pop]得正[先进先出]）
 
@@ -642,8 +638,6 @@ https://www.nowcoder.com/questionTerminal/d77d11405cc7470d82554cb392585106
 ….
 依次执行，最后辅助栈为空。如果不为空说明弹出序列不是该栈的弹出顺序。 
 
-
-
 #### **考察内容：**
 
 栈

docs/cs-basics/data-structure/bloom-filter.md

@@ -6,18 +6,18 @@
 2. 布隆过滤器的原理介绍。
 3. 布隆过滤器使用场景。
 4. 通过 Java 编程手动实现布隆过滤器。
-5. 利用Google开源的Guava中自带的布隆过滤器。
+5. 利用 Google 开源的 Guava 中自带的布隆过滤器。
 6. Redis 中的布隆过滤器。
 
 ### 1.什么是布隆过滤器？
 
 首先，我们需要了解布隆过滤器的概念。
 
-布隆过滤器（Bloom Filter）是一个叫做 Bloom 的老哥于1970年提出的。我们可以把它看作由二进制向量（或者说位数组）和一系列随机映射函数（哈希函数）两部分组成的数据结构。相比于我们平时常用的的 List、Map 、Set 等数据结构，它占用空间更少并且效率更高，但是缺点是其返回的结果是概率性的，而不是非常准确的。理论情况下添加到集合中的元素越多，误报的可能性就越大。并且，存放在布隆过滤器的数据不容易删除。
+布隆过滤器（Bloom Filter）是一个叫做 Bloom 的老哥于 1970 年提出的。我们可以把它看作由二进制向量（或者说位数组）和一系列随机映射函数（哈希函数）两部分组成的数据结构。相比于我们平时常用的的 List、Map 、Set 等数据结构，它占用空间更少并且效率更高，但是缺点是其返回的结果是概率性的，而不是非常准确的。理论情况下添加到集合中的元素越多，误报的可能性就越大。并且，存放在布隆过滤器的数据不容易删除。
 
 ![布隆过滤器示意图](https://my-blog-to-use.oss-cn-beijing.aliyuncs.com/2019-11/布隆过滤器-bit数组.png)
 
-位数组中的每个元素都只占用 1 bit ，并且每个元素只能是 0 或者 1。这样申请一个 100w 个元素的位数组只占用  1000000Bit / 8 = 125000 Byte = 125000/1024 kb ≈ 122kb 的空间。
+位数组中的每个元素都只占用 1 bit ，并且每个元素只能是 0 或者 1。这样申请一个 100w 个元素的位数组只占用 1000000Bit / 8 = 125000 Byte = 125000/1024 kb ≈ 122kb 的空间。
 
 总结：**一个名叫 Bloom 的人提出了一种来检索元素是否在给定大集合中的数据结构，这种数据结构是高效且性能很好的，但缺点是具有一定的错误识别率和删除难度。并且，理论情况下，添加到集合中的元素越多，误报的可能性就越大。**
 
@@ -35,11 +35,9 @@
 
 举个简单的例子：
 
-
-
 ![布隆过滤器hash计算](https://my-blog-to-use.oss-cn-beijing.aliyuncs.com/2019-11/布隆过滤器-hash运算.png)
 
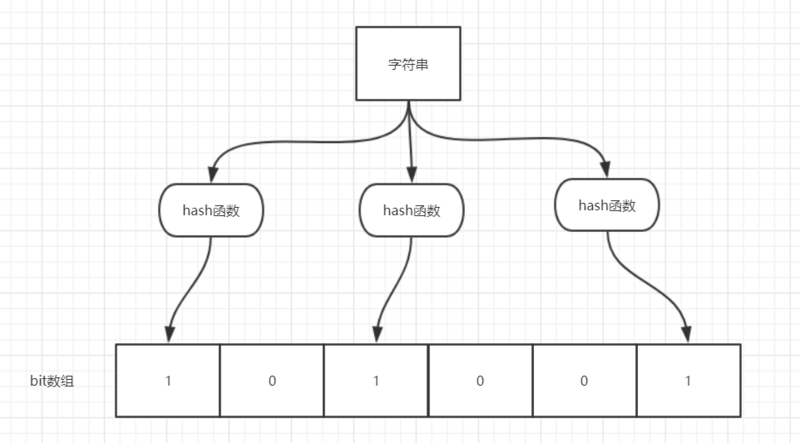
-如图所示，当字符串存储要加入到布隆过滤器中时，该字符串首先由多个哈希函数生成不同的哈希值，然后在对应的位数组的下表的元素设置为 1（当位数组初始化时 ，所有位置均为0）。当第二次存储相同字符串时，因为先前的对应位置已设置为 1，所以很容易知道此值已经存在（去重非常方便）。
+如图所示，当字符串存储要加入到布隆过滤器中时，该字符串首先由多个哈希函数生成不同的哈希值，然后将对应的位数组的下标设置为 1（当位数组初始化时，所有位置均为 0）。当第二次存储相同字符串时，因为先前的对应位置已设置为 1，所以很容易知道此值已经存在（去重非常方便）。
 
 如果我们需要判断某个字符串是否在布隆过滤器中时，只需要对给定字符串再次进行相同的哈希计算，得到值之后判断位数组中的每个元素是否都为 1，如果值都为 1，那么说明这个值在布隆过滤器中，如果存在一个值不为 1，说明该元素不在布隆过滤器中。
 
@@ -49,7 +47,7 @@
 
 ### 3.布隆过滤器使用场景
 
-1. 判断给定数据是否存在：比如判断一个数字是否存在于包含大量数字的数字集中（数字集很大，5亿以上！）、 防止缓存穿透（判断请求的数据是否有效避免直接绕过缓存请求数据库）等等、邮箱的垃圾邮件过滤、黑名单功能等等。
+1. 判断给定数据是否存在：比如判断一个数字是否存在于包含大量数字的数字集中（数字集很大，5 亿以上！）、 防止缓存穿透（判断请求的数据是否有效避免直接绕过缓存请求数据库）等等、邮箱的垃圾邮件过滤、黑名单功能等等。
 2. 去重：比如爬给定网址的时候对已经爬取过的 URL 去重。
 
 ### 4.通过 Java 编程手动实现布隆过滤器
@@ -147,15 +145,15 @@ public class MyBloomFilter {
 测试：
 
 ```java
-        String value1 = "https://javaguide.cn/";
-        String value2 = "https://github.com/Snailclimb";
-        MyBloomFilter filter = new MyBloomFilter();
-        System.out.println(filter.contains(value1));
-        System.out.println(filter.contains(value2));
-        filter.add(value1);
-        filter.add(value2);
-        System.out.println(filter.contains(value1));
-        System.out.println(filter.contains(value2));
+String value1 = "https://javaguide.cn/";
+String value2 = "https://github.com/Snailclimb";
+MyBloomFilter filter = new MyBloomFilter();
+System.out.println(filter.contains(value1));
+System.out.println(filter.contains(value2));
+filter.add(value1);
+filter.add(value2);
+System.out.println(filter.contains(value1));
+System.out.println(filter.contains(value2));
 ```
 
 Output:
@@ -170,15 +168,15 @@ true
 测试：
 
 ```java
-        Integer value1 = 13423;
-        Integer value2 = 22131;
-        MyBloomFilter filter = new MyBloomFilter();
-        System.out.println(filter.contains(value1));
-        System.out.println(filter.contains(value2));
-        filter.add(value1);
-        filter.add(value2);
-        System.out.println(filter.contains(value1));
-        System.out.println(filter.contains(value2));
+Integer value1 = 13423;
+Integer value2 = 22131;
+MyBloomFilter filter = new MyBloomFilter();
+System.out.println(filter.contains(value1));
+System.out.println(filter.contains(value2));
+filter.add(value1);
+filter.add(value2);
+System.out.println(filter.contains(value1));
+System.out.println(filter.contains(value2));
 ```
 
 Output:
@@ -190,61 +188,62 @@ true
 true
 ```
 
-### 5.利用Google开源的 Guava中自带的布隆过滤器
+### 5.利用 Google 开源的 Guava 中自带的布隆过滤器
 
 自己实现的目的主要是为了让自己搞懂布隆过滤器的原理，Guava 中布隆过滤器的实现算是比较权威的，所以实际项目中我们不需要手动实现一个布隆过滤器。
 
 首先我们需要在项目中引入 Guava 的依赖：
 
 ```java
-        <dependency>
-            <groupId>com.google.guava</groupId>
-            <artifactId>guava</artifactId>
-            <version>28.0-jre</version>
-        </dependency>
+<dependency>
+    <groupId>com.google.guava</groupId>
+    <artifactId>guava</artifactId>
+    <version>28.0-jre</version>
+</dependency>
 ```
 
 实际使用如下：
 
-我们创建了一个最多存放 最多 1500个整数的布隆过滤器，并且我们可以容忍误判的概率为百分之（0.01）
+我们创建了一个最多存放 最多 1500 个整数的布隆过滤器，并且我们可以容忍误判的概率为百分之（0.01）
 
 ```java
-        // 创建布隆过滤器对象
-        BloomFilter<Integer> filter = BloomFilter.create(
-                Funnels.integerFunnel(),
-                1500,
-                0.01);
-        // 判断指定元素是否存在
-        System.out.println(filter.mightContain(1));
-        System.out.println(filter.mightContain(2));
-        // 将元素添加进布隆过滤器
-        filter.put(1);
-        filter.put(2);
-        System.out.println(filter.mightContain(1));
-        System.out.println(filter.mightContain(2));
+// 创建布隆过滤器对象
+BloomFilter<Integer> filter = BloomFilter.create(
+    Funnels.integerFunnel(),
+    1500,
+    0.01);
+// 判断指定元素是否存在
+System.out.println(filter.mightContain(1));
+System.out.println(filter.mightContain(2));
+// 将元素添加进布隆过滤器
+filter.put(1);
+filter.put(2);
+System.out.println(filter.mightContain(1));
+System.out.println(filter.mightContain(2));
 ```
 
-在我们的示例中，当`mightContain（）` 方法返回*true*时，我们可以99％确定该元素在过滤器中，当过滤器返回*false*时，我们可以100％确定该元素不存在于过滤器中。
+在我们的示例中，当`mightContain()` 方法返回 _true_ 时，我们可以 99％确定该元素在过滤器中，当过滤器返回 _false_ 时，我们可以 100％确定该元素不存在于过滤器中。
 
 **Guava 提供的布隆过滤器的实现还是很不错的（想要详细了解的可以看一下它的源码实现），但是它有一个重大的缺陷就是只能单机使用（另外，容量扩展也不容易），而现在互联网一般都是分布式的场景。为了解决这个问题，我们就需要用到 Redis 中的布隆过滤器了。**
 
 ### 6.Redis 中的布隆过滤器
 
-#### 6.1介绍
+#### 6.1 介绍
 
 Redis v4.0 之后有了 Module（模块/插件） 功能，Redis Modules 让 Redis 可以使用外部模块扩展其功能 。布隆过滤器就是其中的 Module。详情可以查看 Redis 官方对 Redis Modules 的介绍 ：https://redis.io/modules
 
-另外，官网推荐了一个 RedisBloom  作为 Redis 布隆过滤器的 Module,地址：https://github.com/RedisBloom/RedisBloom. 其他还有：
+另外，官网推荐了一个 RedisBloom 作为 Redis 布隆过滤器的 Module，地址：https://github.com/RedisBloom/RedisBloom 
+其他还有：
 
-- redis-lua-scaling-bloom-filter （lua 脚本实现）：https://github.com/erikdubbelboer/redis-lua-scaling-bloom-filter
-- pyreBloom（Python中的快速Redis 布隆过滤器） ：https://github.com/seomoz/pyreBloom
+- redis-lua-scaling-bloom-filter（lua 脚本实现）：https://github.com/erikdubbelboer/redis-lua-scaling-bloom-filter
+- pyreBloom（Python 中的快速 Redis 布隆过滤器） ：https://github.com/seomoz/pyreBloom
 - ......
 
 RedisBloom 提供了多种语言的客户端支持，包括：Python、Java、JavaScript 和 PHP。
 
-#### 6.2使用Docker安装
+#### 6.2 使用 Docker 安装
 
-如果我们需要体验 Redis 中的布隆过滤器非常简单，通过 Docker  就可以了！我们直接在 Google 搜索**docker redis bloomfilter** 然后在排除广告的第一条搜素结果就找到了我们想要的答案（这是我平常解决问题的一种方式，分享一下），具体地址：https://hub.docker.com/r/redislabs/rebloom/ （介绍的很详细 ）。
+如果我们需要体验 Redis 中的布隆过滤器非常简单，通过 Docker 就可以了！我们直接在 Google 搜索 **docker redis bloomfilter** 然后在排除广告的第一条搜素结果就找到了我们想要的答案（这是我平常解决问题的一种方式，分享一下），具体地址：https://hub.docker.com/r/redislabs/rebloom/ （介绍的很详细 ）。
 
 **具体操作如下：**
 
@@ -252,35 +251,35 @@ RedisBloom 提供了多种语言的客户端支持，包括：Python、Java、Ja
 ➜  ~ docker run -p 6379:6379 --name redis-redisbloom redislabs/rebloom:latest
 ➜  ~ docker exec -it redis-redisbloom bash
 root@21396d02c252:/data# redis-cli
-127.0.0.1:6379> 
+127.0.0.1:6379>
 ```
 
-#### 6.3常用命令一览
+#### 6.3 常用命令一览
 
->  注意：   key:布隆过滤器的名称，item : 添加的元素。
+> 注意： key : 布隆过滤器的名称，item : 添加的元素。
 
-1. **`BF.ADD `**：将元素添加到布隆过滤器中，如果该过滤器尚不存在，则创建该过滤器。格式：`BF.ADD {key} {item}`。
-2. **`BF.MADD `** : 将一个或多个元素添加到“布隆过滤器”中，并创建一个尚不存在的过滤器。该命令的操作方式`BF.ADD`与之相同，只不过它允许多个输入并返回多个值。格式：`BF.MADD {key} {item} [item ...]` 。
-3. **`BF.EXISTS` ** : 确定元素是否在布隆过滤器中存在。格式：`BF.EXISTS {key} {item}`。
+1. **`BF.ADD`**：将元素添加到布隆过滤器中，如果该过滤器尚不存在，则创建该过滤器。格式：`BF.ADD {key} {item}`。
+2. **`BF.MADD`** : 将一个或多个元素添加到“布隆过滤器”中，并创建一个尚不存在的过滤器。该命令的操作方式`BF.ADD`与之相同，只不过它允许多个输入并返回多个值。格式：`BF.MADD {key} {item} [item ...]` 。
+3. **`BF.EXISTS`** : 确定元素是否在布隆过滤器中存在。格式：`BF.EXISTS {key} {item}`。
 4. **`BF.MEXISTS`** ： 确定一个或者多个元素是否在布隆过滤器中存在格式：`BF.MEXISTS {key} {item} [item ...]`。
 
 另外，`BF.RESERVE` 命令需要单独介绍一下：
 
 这个命令的格式如下：
 
-`BF.RESERVE {key} {error_rate} {capacity} [EXPANSION expansion] `。
+`BF.RESERVE {key} {error_rate} {capacity} [EXPANSION expansion]`。
 
 下面简单介绍一下每个参数的具体含义：
 
 1. key：布隆过滤器的名称
-2. error_rate :误报的期望概率。这应该是介于0到1之间的十进制值。例如，对于期望的误报率0.1％（1000中为1），error_rate应该设置为0.001。该数字越接近零，则每个项目的内存消耗越大，并且每个操作的CPU使用率越高。
-3. capacity:  过滤器的容量。当实际存储的元素个数超过这个值之后，性能将开始下降。实际的降级将取决于超出限制的程度。随着过滤器元素数量呈指数增长，性能将线性下降。
+2. error_rate : 期望的误报率。该值必须介于 0 到 1 之间。例如，对于期望的误报率 0.1％（1000 中为 1），error_rate 应该设置为 0.001。该数字越接近零，则每个项目的内存消耗越大，并且每个操作的 CPU 使用率越高。
+3. capacity: 过滤器的容量。当实际存储的元素个数超过这个值之后，性能将开始下降。实际的降级将取决于超出限制的程度。随着过滤器元素数量呈指数增长，性能将线性下降。
 
 可选参数：
 
-- expansion：如果创建了一个新的子过滤器，则其大小将是当前过滤器的大小乘以`expansion`。默认扩展值为2。这意味着每个后续子过滤器将是前一个子过滤器的两倍。
+- expansion：如果创建了一个新的子过滤器，则其大小将是当前过滤器的大小乘以`expansion`。默认扩展值为 2。这意味着每个后续子过滤器将是前一个子过滤器的两倍。
 
-#### 6.4实际使用
+#### 6.4 实际使用
 
 ```shell
 127.0.0.1:6379> BF.ADD myFilter java
@@ -294,4 +293,3 @@ root@21396d02c252:/data# redis-cli
 127.0.0.1:6379> BF.EXISTS myFilter github
 (integer) 0
 ```
-

docs/cs-basics/data-structure/pictures/树/中序遍历.drawio

@@ -0,0 +1 @@
+<mxfile host="Electron" modified="2021-05-29T04:49:35.956Z" agent="5.0 (Macintosh; Intel Mac OS X 10_16_0) AppleWebKit/537.36 (KHTML, like Gecko) draw.io/13.4.5 Chrome/83.0.4103.122 Electron/9.1.0 Safari/537.36" etag="C0yATZcJo9RVnSwHs8Dx" version="13.4.5" type="device"><diagram id="EVHAlbz1pNCSG6H1n3D9" name="Page-1">7Vtbk6I4FP41eZwukgBJHr1g727tVk1VV+30PNKSVmbQuIit7q/fBAISBLVbFHfa8sHkJORyzpcv5xwR4MFs8xj7i+lfIuARQFawAXgIEILQcuWXkmwzCWMkE0ziMNCddoKn8F+uhZaWrsKAL42OiRBREi5M4VjM53ycGDI/jsXa7PYqInPWhT/he4KnsR/tS7+FQTLNpBSRnfw3Hk6m+czQZVnLzM87650sp34g1iUR9gAexEIkWWm2GfBIKS/XS/bcqKG1WFjM58kpD6yenT8ev/39O3VCf/C2ZpuF7X/Ro7z50UpvGCA3kuP1X9SSk63Wg/vPSq2z/yrmyZdlaqWe7ICcxWbXKEsT9d3Lx5CLecmFWgnFiEiuThpRVvrraZjwp4U/Vi1riSMpmyazSNagLPrLRWbZ13DDA7WIMIoGIhJxOhB+feXueCzlyyQWP3mpJSDsxbKKyd94nPBNo/pgYRSJZi5mPIm3sot+gGBtRw1kzHR9XYKFFk1LiMhlvgbipBh5ZytZ0OZ6h+lQjemqKp4HPXUGZG0u5txUq9x3vH0uV76XK0O1b6uobXUtm4MHe6emoke5DrGKx/zABrA+zn484ckxjO7bpaR3p0bvuSzmkZ+Eb+Zy64yhZ/gqQrmRndktYpidWBV7ZtvUT5WPX3Ug5jwgaiMCkU1sN1+JHtYm1GzF5iyZkvZmSYFT6OTjWMKNNLBc+POPM0GJTDLBoJ4aClk23a/BGJSajGF3zRj2tazc/0RWdq0bs7JzLSsPP5GVHWRa2SEdW9m9lpUfP5GVmXtjVibn+nibMHkulb/nPp0s7xw8Vcn9u8IrLCpX9grt/4NX6FaAQuAHvUKKqIk4hq7q+NFzAVYbRFhH4JLD0irBEh6EZQcAc7oEGKneN+yjYYdDD4UdrNOwg52JvhZR4Z6ICtwlKiiCDy7GDrapdEgQNI3pUPjAIGO27AZtNw9c301J2D2AGIdada1XAkxOs5d3e7xP5Pa49MbcHliXljzX7zl8wdT7Pccusi78HqvelldyfMw8FWQmcCB8INAhiBIHOZhWhj/5zrJqh8nvLFq7hGsxEGpkIEU0LTKQfYSBsukaGEiSQWIeCZNB9JEp040W+VE4mcvqWCKYS3lfUUs49qOebpiFQRA1cVssVvNAMdmwLW5ilfSKtc9Ndg3e0cW4qTlX2jIA0B0AilOcyuXUOQCa06gtA8C9AyD1R28NAM0Z1pYBAO8ASC/8CgBo1wBw971R6QI+6arWoqkHESdTMRFzP/pTiIU2yA+eJFv9zoO/SkRDbsV6cDpKxuVvXHwwGXeys3meOeqypBcJCkefKCik1q0Fha3lKt+V2n5/Cr3N80dOPICdpqWgZQZsxIwKXYjrWt8bFbKDmUwJzy7zUnWZzIu4BM7dJZAthNyYS5APfHkAkDsAFBlUg4LOAdD8JmXLAMB3AKhLxb41ADQnBs/zQod9rzcalF/DOOhm/jIWJpXf2N3OLYz3/c1LhH35j+NZ1HdtlzPH8VGXM+vYVdCHarJwngP6Huh5wLOBjNV6EHguYBZgA+AhQNOCycnjInbanToZXzGG8f5BfAyT6epFjUk9wCjwGKAEMDkLVZOq6RxAKWCoiY31KoYFp8en0AK0a+8FORnrA+apQs8GdNjKJr8OR0dXL/crNSA9EbXfEWCuXotUvlIFAT1c0glRBUZSWwxAv5d2HqUFojrkx/rmOCzyX3jU98c/J6m8OrlUjT7D0Nb1UijeTz8theLQZEIb7zNhQXtnUqGs7v6SkoVHuz/2YO8/</diagram></mxfile>

docs/cs-basics/data-structure/pictures/树/中序遍历2.drawio

@@ -0,0 +1 @@
+<mxfile host="Electron" modified="2021-05-29T05:07:59.001Z" agent="5.0 (Macintosh; Intel Mac OS X 10_16_0) AppleWebKit/537.36 (KHTML, like Gecko) draw.io/13.4.5 Chrome/83.0.4103.122 Electron/9.1.0 Safari/537.36" etag="kfCcmOqPzhMfcE_oloNB" version="13.4.5" type="device"><diagram id="I4wgBHwh16mVk95mslPn" name="Page-1">5ZhNc5swEIZ/jY/uYLDBHGPsuIdmpmMfmhxlkEGtYKkQBvLrK1niq46bJm0Zpj6hfSWtpH12NSMmlheXW4bS6AECTCemEZQTaz0xzdnMsMVHKpVSXNdRQshIoAe1wp48Yy0aWs1JgLPeQA5AOUn7og9Jgn3e0xBjUPSHHYH2V01RiC+EvY/opfqFBDxS6tJ0Wv0jJmFUrzyzXdUTo3qwPkkWoQCKjmRtJpbHALhqxaWHqQxeHRc17/5Kb7MxhhP+OxN22UPg7CLH2z06MV1Pt0bxPNVeTojm+sAT06bC3+ogt8wrHQf7ey73uTpCwqfZmdKdGGAu0rLtFK1Qfu9qH2Izh1rUQWg8mmJ3AqIwVkVEON6nyJc9hcgjoUU8psKaiSbKUkX2SEocyE0QSj2gwM6OrOMR274v9Iwz+IY7PYHjHgyjWfyEGcfl1fDNGigimzHEmLNKDNET7DojdSLPa7vopIWWok5G1BrSiRg2nltWoqFxvQGdeRVdlqLk/fQ6CaAE72WcjaaW+z8oO+7IKFtDUV7dEOW5NTLK86Eor2+IsjUfGeXFUJS3N0R56bjjomwPRXlzQ5QX5shq2bmMaCAeDtpMIJGhZZAngQzaWoYBGI8ghATRTwCpDu9XzHmlnz0o59APvogOqx7l/A+L2nzq9q1L7VxZlbbey0ie4deExJEhZz5+/U3BEQsxf23cJXGGKeLk1N/HX+e3HKpK72+oSh1jZFXqDlOlJeGdIhXWU12Vot2WqDT+fYX+QUXpqZ+BCI/ty/enu7e5i2sX6kbQs7p/IN7qSF0ZF47O6JvzvJQNwmx/pKjh7e8oa/MD</diagram></mxfile>

docs/cs-basics/data-structure/pictures/树/先序遍历.drawio

@@ -0,0 +1 @@
+<mxfile host="Electron" modified="2021-05-29T04:48:12.234Z" agent="5.0 (Macintosh; Intel Mac OS X 10_16_0) AppleWebKit/537.36 (KHTML, like Gecko) draw.io/13.4.5 Chrome/83.0.4103.122 Electron/9.1.0 Safari/537.36" etag="hkPLy-zMIJkJ0CVjwNx3" version="13.4.5" type="device"><diagram id="2ziagjPv7Po7rTjOazMm" name="Page-1">7Vtbk6I4FP41eZwuIDfyKIq9D7tVU9u1tTOPKGllGo2L2Or8+k0kIEFQ2xvOtOWDyUnI5ZwvJ985IoDdyeo5CWbjv0TIY+BY4QrAHnAc27aI/FKSdSZhjGaCURKFutNW8BL95FpoaekiCvnc6JgKEafRzBQOxXTKh6khC5JELM1uryI2Z50FI74jeBkG8a703yhMx5nUdehW/gePRuN8ZpuwrGUS5J31TubjIBTLkgj6AHYTIdKsNFl1eayUl+sle67f0FosLOHT9JgHEuvvH2+rZPbTI6O56/T+WTrPX/Qo70G80BsGDonleN5ALTldaz2Q/xZqnd6rmKZf5hsrdWQHB89W20ZZGqnvTj6GXMwgF2olFCM6cnXSiLLiLcdRyl9mwVC1LCWOpGycTmJZs2UxmM8yy75GKx6qRURx3BWxSDYDwddXToZDKZ+niXjjpZaQsoFlFZO/8yTlq0b12YVRJJq5mPA0Wcsu+gGCtB01kCHW9WUJFlo0LiEilwUaiKNi5K2tZEGb6wOmc2pMV1XxNOyoMyBrUzHlplrlvpP1t3Lle7nSU/u2itpa17I5eLhzaip6lOsQi2TI92wA6uMcJCOeHsLorl1Kesc1es9lCY+DNHo3l1tnDD3DVxHJjWzNblPD7IRU7JltUz9VPn6VgaiFnxwXOdR2EEUkX4keFkHXbIXmLJmSdmbZAKfQyelYgo1uYD4Lpqd7gpIzyQTdetdQyLLpfg+PQZnpMVDbHgPdysreJ7Iytu/MyvhWVu59IisjaFoZw5atTG5l5edPZGWX3pmV6bkcbxWl30rl7zmnk+UtwVOVnN8VrLCo3JgVol+BFeIKUAg9lRVC10Qcdm5K/NxzAVYbRFgH4JLD0irB0t4LyxYAhtsEGKneN/hEgBHi7gs7cKthBzsTfRdEBTkSFbBNVFBoPxEIMUQulhe4bRoTI/uJ2YwhV7YgYtETXRIiexCDkVXXeiPA5Fz7+rTH/0S0B7M7oz12XVryXN6z/4Kp5z2HLrI2eI9Vb8sbER/XuDBsZl4n1H6iNqaSSGOJIrcy/NF3ll07TD4Jql3CrTyQ0+iBlKO5oAeyD3igbLoGDySdQWoeCdOD6CNTdjdaFMTRaCqrQ4lgLuWeci3RMIg7umEShWHc5NsSsZiGypP1LpV2typpd7Lrm1AN3p2r+abmXOmFAeA8AKCMS0wAoNYB0JxGvTAA8AMAGz56bwBozrBeGADwAQDl8qv0FLUNALLLRiUFfNFVrUVTDyJJx2IkpkH8pxAzbZAfPE3X+p2HYJGKhtyK9YRbSsblb1ycmIw7mmyeZ466LOlVgsL+JwoKqX1vQeHFcpUfSm1/PIV+yfNHjzyAraalmBmvUTMoxBTWtX40KHT3JjIlOttMS9UlMq/CCMiDEcgW4t4ZI8gHvj4A6AMAyhmgewNA84uUFwYAegAAlH4PuxsANOcFzyOhHa/nd/vltzD2sszfxsKk+hN76xaGu3TzGlFf/tt4FvTdmnHmOD7IOLOObcV8Tk0SzsfA80HHBz4CMlTr2MAngFmAdYHvAHdTMH3ysAidtqdOhleMQbh7EJ+jdLwYqDFdHzAX+Ay4FDA5i6smVdNh4LqAOU3eWK+iV/j05Bi3YKPae0FOxjzAfFXoIOD2LrLJr73+wdXL/UoNSCai9tsHjOi1SOUrVVDQgSWdUFVgdGOLLvA6m879TYGqDjmVuzsfFgcDHnvB8G20kVcnl6rRZ9hGul6KxL3N50KReOVdkCIfVvKEhds70xXK6vYfKVl4tP1fD/T/Bw==</diagram></mxfile>

docs/cs-basics/data-structure/pictures/树/后序遍历.drawio

@@ -0,0 +1 @@
+<mxfile host="Electron" modified="2021-05-29T05:13:41.075Z" agent="5.0 (Macintosh; Intel Mac OS X 10_16_0) AppleWebKit/537.36 (KHTML, like Gecko) draw.io/13.4.5 Chrome/83.0.4103.122 Electron/9.1.0 Safari/537.36" etag="yfEGH1DOOH5Vsjp4lb7P" version="13.4.5" type="device"><diagram id="FIgDf6u-rJ36MxwX6W4d" name="Page-1">7VvLluI2EP0aLacPlqzXEoPpLJKcySHJPHZurAZnDCLGdEN/fSQsGwtsoHmZTHNYIJVkPaqurqoKA1BnvHhMgunoNxmKGMBWuACoCyB0nBZRX1qyzCSc00wwTKLQdFoL+tGbMMKWkc6jUMysjqmUcRpNbeFATiZikFqyIEnkq93tWcb2rNNgKLYE/UEQb0u/RGE6yqQM0rX8FxENR/nMDuFZyzjIO5udzEZBKF9LIuQD1EmkTLPSeNERsVZerpfsuV5Na7GwREzSQx6I2vhvtYG/fv/jz7cvuP+9P38bfTKjvATx3GwYQBKr8bwnveR0afRA/p3rdXrPcpJ+mq2s1FYdIJ4u1o2qNNTf7XwMtZinXGiUUIwI1eqUEVXFex1FqehPg4FueVU4UrJROo5VzVHFYDbNLPscLUSoFxHFcUfGMlkNhJ6fBRkMlHyWJvKHKLWElD+1WsXkLyJJxaJWfU5hFIVmIcciTZaqi3mA5HY0QIbU1F9LsDCiUQkRuSwwQBwWI69tpQrGXO8wHaww3aaKJ2FbnwFVm8iJsNWq9p0sv5Yr38qVrt53q6gtTS2bQ4Rbp2ZDj2odcp4MxI4NIHOcg2Qo0n0Y3bZLSe+4Qu+5LBFxkEYv9nKrjGFm+CwjtZHC7DjnK2N2vGnPbJvmqfLx2xiIMPwAmQupA13qknwlZliEmd2K7FkyJW3NsgJOoZPjsYRqaWA2DSbHM0GJTDJBp5oaClk23c/BGJTajIGaZgz3Wlb2PpCVXX5jVsbXsnL3I1nZsa3s4oatTK5l5ccPZGWGb8zK9FQfbxGlX0vlb7lPp8prB09Xcv+u8AqLypW9Qvd/4RVuAAXzI71C6jAbcRRe1fFjpwKsMoho7YFLDstWCZbOTlg2ADDcJMDI5n1Djw07XLYr7KCNhh38RPSdERXkQFSgJlFBHeeBIISRy7C6wB3bmC5xHrjDuctUi0ta9EhKgmQHYtS4TSImPxaX93v8D+T3YHpjfo9TlZc81fHZfcNUOz77brImHJ9WtS2v5PkQ68ZwuH2fcOeBOphCRjHEiG0MfygF4eph8kmql3AtBoK1DKSJ5owMRPcwUDZdDQMpMkjtI2EziDkyZboxoiCOhhNVHSgECyX3NLVEgyBum4ZxFIZxHbclcj4JNZN1z8VNzOamgnRKeHcr8A4vxk31ydIzAwDdAaCN69oAQI0DoD6PemYAkDsAVg7prQGgPsV6ZgA4dwCAUkp9HYM0DACy7Y0qF7BvqkaLth5kko7kUE6C+Fcpp8Yg/4g0XZqXHoJ5KmuSK60H3FA2Ln/l4shs3MHO5mnmqEqTXiQo7H2goJDwWwsKz5asfFdu+/059HOeP3rgAWw0L8XseI3aQaHLkdXKjkxMsZ2pTAXPRhNTVbnMi/gE7t0n0OxEbswnyAe+PADwHQCaDeCtAaD+XcozAwDeAaDvLnRrAKjPDJ7mhnZ9r/fYKb9Vu9PP/GksTDZ/ZW/cwmjb4bxE3Jf/PJ6Ffdf2OXMc7/U5s45NRX2wIg3nY+D5oO0D3wUqWGs7wCdAxTG8A3wI2Kpgc/KgCJ7Wp04FWJwjtH0QH6N0NH/SYzIfcAZ8DpQzy9UsTE+qp8OAMcBhHRubVXQLTk8OoQXHrbwX1GTcA9zXhbYLWPcsm/zc7e1dvdqv0oBHV/vtAU7MWpTytSooaKOSTqgucLqyRQd47VXn3qpAdYc8Yrw5DouDJxF7weDHcCXfnFypxpxhxzX1UizurT6XicUR3GbCgvZOpEJVXf8pJQuP1n/tQf5/</diagram></mxfile>

docs/cs-basics/data-structure/pictures/树/完全二叉树.drawio

@@ -0,0 +1 @@
+<mxfile host="Electron" modified="2021-09-13T02:02:53.966Z" agent="5.0 (Macintosh; Intel Mac OS X 10_16_0) AppleWebKit/537.36 (KHTML, like Gecko) draw.io/13.4.5 Chrome/83.0.4103.122 Electron/9.1.0 Safari/537.36" etag="dKxw4KtKSwJUg7jbYpyW" version="13.4.5" type="device"><diagram id="uNQEILGOwt5n9zeOTizL" name="Page-1">5VpLc+I4EP41OoaynpaOPJzsZatSNYedOW0ZWwHvGMwYM8D8+m3bsrGMCQwhhAyVQ9QtoUf3p+5PDYgOZ5un1F9M/05CHSPihBtER4gQjB0B/3LNttRIRUrFJI1CM2in+BL90kbpGO0qCvXSGpglSZxFC1sZJPO5DjJL56dpsraHvSSxverCn+g9xZfAj/e1/0RhNjWnIO5O/5eOJtNqZSxU2TPzq8HmJMupHybrhop6iA7TJMnK1mwz1HFuvMou5eceD/TWG0v1PDvlA5GOgn9/JWv68PTfdumwH6Px8sHM8tOPV+bAiIgY5huMoTHJG/Dfny2gMR8vF6VcDHhJYF04VrY1thI/VknV8bAsPNmHAYQvNrvOalanmgY2XM5Ur1apGzsg1kIEDgb+B2GwnkaZ/rLwg7xnDRAE3TSbxSBhaPrLRQmKl2ijw3xvURwPkzhJi4noy4sWQQD6ZZYm33WjJ3TV2HHqxZtmrmym00xvGipj9iedzHSWbmGI6aXCQMDcAVLJ6waijGraAFOl8w2GJ/XMOzdDw3j6N7xOOrzeNvE87OfXB6R5Mte2WcEU6fZrU/jWFEb5uZ1a2hrpgrZfJqs00K+ckJpQ4acTnR3Hvw6tKLDvyYaneIenKl2qYz+Lftqxo8t9ZoXnJCouUQUUZgOF8xYCynObTzXvensi1ZrIaU1UGmZvogJN9bHPBxg9KaxcIIyQOwojTArLqZR/cBhhB728XPjz8526hxXc7c5aVy73Z3iZUOe2vMyvdZfpHd1lzG0vM/rBXhbX8jK/Iy8zzG7Ly+5bid8myr422t8qogftHevLhYr01VSxFm6NKrI/gyqKM6kid6SNUUauShXlWyHZ+RZxjgCsArLTADJ+Fci3CEl+W5Bs57SzXy9S9ohkxMWEuUwQTFuMqLv7SoBVlwLszUZEcSL86E3Bj1PVE5RyyiQH8oGxDUasegorxST0MOG450GTMfsNxtl1H9ZVWfT931zsjt5cFN8YG8ddddm3ErXX81t3WDqWR28xK1bOvJG4RB0rXWFlJzMX91zMXSJdDiFMtqY/OWXSzmmqRVjnFq4Vs8jBmHXht6W4o7clF7cWs7qKvm9n8pcnRjX372GXNx+yPaeWD8RIEJ51GoHBdGp058ez6l58Mp7FlOwpIYjCDgOqJbkNQ+H0uMvyb0g5kVxwcV5A49QmWuzaROtwcfvCQcu9o6DV/lrqo2vb+HBx+8J0Wt4Rna5/8tCuTX2Ym7uq2+e92Xv805SZjhNl1plYTkhd/CMTEJbwlFc113WlXWTnGBK50ygPnZmBsBA9Lg5WoTilPUZ3u7gyp36PSv7VkLkHuONQ5Z8BmZRdBZntcsVe7f+dwSc6wOdxNPBQ30MeQ4NH1MfIEwjSvRoijyBZNGy6FNSI2SVPQJVSlO7n06com67G+ZzSQ0oiTyHpIgWryHzRfDmOpESKHGJTZhejOjOnp2R3zDqzOyymBkh5eaPPkBxd5JDPo8eju4fzggWANObnfURKmL2A8XNTuKhPGzZx84ZyC18M0aBfDH4sGm4+oMq4jagBOT6zQ4V9wU0oaUYDo/LjaDIHMYDrnj+PBjljiAI/7puOWRSG8SEWkyareZhzliLYxP5YxwM/+D4p9O3FwTTmp6KQw0q5EYAGxd+FSoPuccpa851mSCG/T2ZA3P0ctLysux/VUu9/</diagram></mxfile>

docs/cs-basics/data-structure/pictures/树/平衡二叉树.drawio

@@ -0,0 +1 @@
+<mxfile host="Electron" modified="2021-05-29T04:12:43.504Z" agent="5.0 (Macintosh; Intel Mac OS X 10_16_0) AppleWebKit/537.36 (KHTML, like Gecko) draw.io/13.4.5 Chrome/83.0.4103.122 Electron/9.1.0 Safari/537.36" etag="csU4omjrt7oruFe75GcO" version="13.4.5" type="device"><diagram id="1XXsLY0auXVlGK_2y-eQ" name="Page-1">7VnJdpswFP0aL+OjiWmZOEm7SIdzsmjSHQbZcAqIynKM+/UVRmIysR2SYKfuCr0r8TTcq6eHGOFJnH3ibhp8YT6NRgj42QhfjxCCEJjykSPrAnEcqwDmPPRVowq4D/9QBQKFLkOfLhoNBWORCNMm6LEkoZ5oYC7nbNVsNmNRs9fUndMt4N5zo230R+iLoEBtZFX4ZxrOA90zNJ2iJnZ1YzWTReD6bFWD8M0ITzhjoijF2YRG+eLpdSneu32mthwYp4k45IU7eumBOPrJb52v09m3AKzusgvl5cmNlmrCI2RG0t/VVBbmeUE+3TiVhWS6SAt702DGZL9yWmKt1sr8vWS64mKxYfJSNkBGmlWV2ivQbuSAC09lbxqujQA1OkJyYpJ/aVytglDQ+9T18pqVlKDEAhFH0oKy6C7SQhSzMKN+PrYwiiYsYnzjCM9m1PQ8iS8EZ79orca3nCkAZedPlAuaPbvysORTbgTKYir4WjZRL2BTSUDtAaTtVU1RCgpqYtKYqzQ8Lz1XNMuCYvoFrKMO1ttLnPiX+faRVsIS2lxWOW++fqgbj3XjOp83KK21svquPfW3tmhr5eXI2ZJ7dMeUsYodLp9TsW9DbDNZY8roYEpjnEauCJ+aw+2iT/XwnYWbTaSFQppCMYyWAoppqrfqe73tyGk5Ai1HxTpsOdqoqZx2f4Hhg8LKG4QRdEZhhLTUUarlWGGEPMvyInWT/qRuaQV201liRXf/BsslXafCsjHUXsZntJcRaLJM0JFZNodi2Tgjlg10Yixbr038slA81MqPOtGT5Srryw2d9JWpYmmcfKpIPmSqaPZMFQ1gNzVK0KCpov1aSXZ+i4A9AtNCBjUhw51C/hCSNI4pSdI+00hPSRJsj5FNkAURsYiJIG5lRN3VAwnWeRfBnnRENA+UHz6q/Bw8NjE2pDzkuYvKm0etRuCMHeg4xEYQEhNYPbXZErmBh/2y1vei7//RRc7oo6t9Q3f0RA12Xcy+NlPbfcB1Z2r7DtIPcSxC0M3+QKma0TivoNM8zUw4tqBhIdsyZDSxW+4PvvGzO93oTnDnEIaKWWiomGWeUcxqXxSVd7xHi1ldt77/Y1b3ddr+mIVON2YRuDOcvE3MImRnYOwds6RZ/XQtmle/rvHNXw==</diagram></mxfile>

docs/cs-basics/data-structure/pictures/树/斜树.drawio

@@ -0,0 +1 @@
+<mxfile host="Electron" modified="2021-05-29T04:15:40.180Z" agent="5.0 (Macintosh; Intel Mac OS X 10_16_0) AppleWebKit/537.36 (KHTML, like Gecko) draw.io/13.4.5 Chrome/83.0.4103.122 Electron/9.1.0 Safari/537.36" etag="tAGOABOmbL2WRh0a8tL1" version="13.4.5" type="device"><diagram id="vMa7lu0pAO2kmhAGVbwg" name="Page-1">5VhNc9owEP01HMnY+rCtY0LSdibNTKc5NOnN2AJ7KixXiGD667vGsi0bSGlKcTI5sfskrbT73grBCE8WxUcV5smdjLkYIScuRvh6hJDrOh58lMimQhjzK2Cu0thMaoH79Bc3oGPQVRrzZWeillLoNO+CkcwyHukOFiol191pMym6u+bhnO8A91EodtFvaayTCg2Q3+KfeDpP6p1dj1Uji7CebDJZJmEs1xaEb0Z4oqTUlbUoJlyUxavrUq37cGC0OZjimT5mwfT2s7i+U1/V7ePDOLv8TokYj02Up1CsTMIj5AmIdzUFY14a8BkucjCy6TKv/O2EmYR9IS29MbXyfq5kPTBebpm8hAmI5kU7WEd16jBw4CpSs1sNWydAnY0QJAb8g3O1TlLN7/MwKkfWIEHAEr0Q4Llghsu8EsUsLXhcni0VYiKFVNtAeDbjXhQBvtRK/uDWSOyzqeM0mz9xpXlxsPJuwyc0ApcLrtUGppgFxDcSMD2AqPHXlqIMlFhiqrHQaHjeRG5pBsMw/Resoz2s90ucxZdl+4CXyYx3ywp5q82D7TzaznWZt9N4G+O9tPY83mnRXuXh5HKlIv5MytjcHaGac/2nhthl0mKK7mGqxhQXoU6fusfdR5/Z4YtMt01UC4V2hUJxTwFVmmaV3eu9QNTpBiJ9KVV12Am0VVOT9ssFho+6Vk5wjbjv6BqhPXVgPPA1Qg6y/G+k7mgF7afzAPNvm2UP91rXHZhleq5exu+ol323xzIbmGXvXCyT98Qy632f+wOz7A/y8ONFqh8s+9Gy2yWl8yqeiuTIpyJ+VU9FcqqnIjvvUzE4lSQdW5LOkZJ0LUm6b1+SdEhJUoYvPIwpJgGF2991u69Vn10wlzESwAjxHP+FciXBBQoIfIHCz2riod4mqDeKz6plNsj1OqgyvbegTM95VpnBaZRJn1Um/k/KBLf9D7Ga3v4Ti29+Aw==</diagram></mxfile>

docs/cs-basics/data-structure/pictures/树/满二叉树.drawio

@@ -0,0 +1 @@
+<mxfile host="Electron" modified="2021-05-29T04:39:49.228Z" agent="5.0 (Macintosh; Intel Mac OS X 10_16_0) AppleWebKit/537.36 (KHTML, like Gecko) draw.io/13.4.5 Chrome/83.0.4103.122 Electron/9.1.0 Safari/537.36" etag="muDFVz9R5z3fWmbL7Wg8" version="13.4.5" type="device"><diagram id="9pQr6OEqs1j3d8CnLuWx" name="Page-1">5VnLcpswFP0aL+PRG1gmTpq2M5nJTBZNuiNGNkwxogLHOF9fYSSMME5c2/WjXqF7JK4e5+jqCnp4MCnupZ+GDyLgcQ+BoOjh2x5CEAKmHiUyrxDPcypgLKNAN1oCT9E71yDQ6DQKeGY1zIWI8yi1waFIEj7MLcyXUszsZiMR272m/pivAE9DP15Ff0RBHlaoi5wl/pVH49D0DJlX1Ux801jPJAv9QMwaEL7r4YEUIq9Kk2LA43LxzLpU731ZU1sPTPIk3+SFZ4cW19/kzzALJmPy8P39HlxdaS9vfjzVE+4hFit/N6+qMC4L6ulPUlVIXrO0shcNRkL1q6aVz/Vasd9TYSqusgWT16oBommxrDRegXGjBlx5qnszcGMEyOoIqYkp/pVxMwujnD+l/rCsmSkJKizMJ7GyoCr6WVqJYhQVPCjHFsXxQMRCLhzh0Yiz4VDhWS7FL96oCRzvFYC68zcuc16sXXlY86k2AhcTnsu5aqJfwExLQO8BZOxZQ1EaChtiMpivNTyuPS9pVgXN9F+wjjpYby9xElyX20dZiUi4vaxq3nL+3DRemsZtOW9QW3Ntbbv2PFjZoq2VVyMXUznkH0wZ69jhyzHPP9sQq0w2mKIdTBlM8tjPozd7uF306R4eRbTYREYoxBYKpS0FVNPUbzX3etuR13IEWo6qdVhxtFBTPe3tBYY3Cit7CCPogsIIcZlFKqZHDiNkLctZ6ifbk7qiFdhNZ41V3f0fLCMMTotleqi9jC9oL0Nqs0zwkVlmh2KZXhDLBJLTYtnZNfErovy5UX4xiZ4qL7O+0jBJX50q1sbJp4rkLFNFtmWqSIFra5Sgg6aK7q6S7LyLgE8EZoQMGkKGHwr5LCRJjyrJ9pm29e3FdfvIJciBiDiEIYhbGVF39YEE6+1LsOcTEdmG8sPHlB/FXp9hTDFxqUo+ILTFCL2+Bz2PuKqGMOBsJ01C7DsYJYe9WJvPov/+zkUu6M6F4Yll47Dru+yuidrH51t3WPrsHD2LUxGCbvYPdCwC67iCnn2YObDvQOog16EqhLkt9xsfmbjTjemEdA7hUDFr/XeiPd8t2QXdLSk7tZjV9Qlh90x+/4lRnfv3oUObF9k+qO01MVIZj1xGasG41Nge4xncNKAdNc8intv3GEMeBESlWi61ZchAnzqk/ENKkUsZZdsFNIrtRIvsLdFS5vKna9V8+esa3/0B</diagram></mxfile>

docs/cs-basics/data-structure/pictures/树/链式存储二叉树.drawio

@@ -0,0 +1 @@
+<mxfile host="Electron" modified="2021-05-29T04:06:33.188Z" agent="5.0 (Macintosh; Intel Mac OS X 10_16_0) AppleWebKit/537.36 (KHTML, like Gecko) draw.io/13.4.5 Chrome/83.0.4103.122 Electron/9.1.0 Safari/537.36" etag="t34LwBo12ySwl6wqXax5" version="13.4.5" type="device"><diagram id="ox7Zji1cJtBwcgYqQnlA" name="Page-1">7Zxbb9owFMc/DY+bcg95LPQyaUya2kntHl1iiFcTZ8bc+ul3HBxIloXCgMQPFkjEx5fE/h38z3EMPXc4Wz9wlCXfWIxpz7Hidc+97TmObVsBfEjLZmuJonBrmHISq0J7wxN5x8poKeuCxHheKSgYo4JkVeOYpSkei4oNcc5W1WITRqtnzdAU1wxPY0Tr1mcSi2Rr7Tvh3v4Fk2lSnNkOom3ODBWFVU/mCYrZqmRy73rukDMmtkez9RBTOXjFuGzr3Tfk7i6M41QcU2HgfX9xfi98h44e3r/es+dF9PbJUdcmNkWHcQz9V8mUpfAx4GyRxlg2Y0GKcZGwKUsRHTGWgdEG4y8sxEbRQwvBwJSIGVW5cIV88yLrf/aL5E/VXJ64XVdSG5WaC87e8JBRxvOLcy0rCPw+5ExYKkp2fyhfYN92R/ahcZSUac4WfIwPDU1fuRviUywOFfR2NOFrgNkMQx+gIscUCbKsXglS/jjdldsjgwNF7QSCriF4NkE76JKgZwge/modQbDfJUDfADwboOt0STAwBA/PjcdMop0SDA3BswmWbks7IKjEeonoQp3pFglUwwq30Zk8FOhVmsp0VgkR+ClD+WisIB7JRx5xoXh6EgUECgKRFHNVacwoRdmc5K3lsMYJofEIbdhCFOcpUjmuwqlkbUTJNIXjMVCRTQ6WmAsC4cONypiROM6vc0IoLYF27KF145/hGvJEeH3YOeooVQWvCK9UVOb1VXq1j3HsInBJSvFNaF2JftQIGnolCKKPEN2hdHoM8zrSmLPsR+H+0pAxIoHdLWHA5spWJqQmDJHPCzKT4klR95UJwWYqwdXY7BrNB8YfwBuGaijnCR96M4S0vU/DWxbnwDcFBwB/lG1gNBcrPBfX84pT7p0K1zjSM9xreUbhqqWJYSRhXNJf8rUDtPeXs12BAYgJzcP9BGYAnLbMNPo30xLEoFWGdo3hY35aA/F0iOsqwM6YOkawWxPsMNRNsO36wpNR7JYmhqZQSxvJ9oxknw7V1UyzfaPZl6Ooi2gHRrRbE+3+X6Ltel7Xol1fJjOi3dbM0PCQSRvRri/AGdH+EGqomWhHRrQvR1ET0XbqK2BGtK8l2pF2kfbuQY8R7dZFu+mRmC6i7dQX4Yxofwi1YQbobH53jWhfjqIuol1fAzOifS3R9m3dIm2nvinMiHZbM0PDhlxtRLu+CGdE+0OovmaiHRrRvhxFXUTbbEJrT7SDqCrau1/KdCfaZhdad6Kt+Ta0omEj2qdA1Wwfmmv2oV2Qoiai7dbXwIxoX020tds57pqNaJ2JdtOvtrQRbbMR7T+garYRzTUb0S5I8eqiDcn9nxrkeaW/hnDv/gA=</diagram></mxfile>

docs/cs-basics/data-structure/pictures/树/顺序存储.drawio

@@ -0,0 +1 @@
+<mxfile host="Electron" modified="2021-05-29T04:45:41.829Z" agent="5.0 (Macintosh; Intel Mac OS X 10_16_0) AppleWebKit/537.36 (KHTML, like Gecko) draw.io/13.4.5 Chrome/83.0.4103.122 Electron/9.1.0 Safari/537.36" etag="iKUbU63_jbqeO2KKhoI_" version="13.4.5" type="device"><diagram id="781hTf24KyYCwh97XMbf" name="Page-1">7V1dc5s4FP01PDYDSAh49FfSh3amu+nMto8yyDYtRi6WE3t//UogMGCwiSHgjZlkJuiCJXHP0dXVMSgKmKz3TyHerL5Sl/iKrrp7BUwVXdc0FfE/wnKILbZtxoZl6LnyoqPh2fuXSKMqrTvPJdvchYxSn3mbvNGhQUAclrPhMKSv+csW1M+3usFLcmJ4drB/av3Hc9kqtlq6ebR/Jt5ylbSsITs+s8bJxfJOtivs0teMCcwUMAkpZfHRej8hvnBe4pf4c48VZ9OOhSRgdT7w9OMPePm6oQxPv88OwRr9+uvwSY9recH+Tt6woiOf1zeeiy6zg/QD+rMT/RwvaMA+bSOURvwC3djsjyf50VL8HSV18M7ME6N0QlqjznvHQeSF8evKY+R5gx1x5pXziNtWbO3zksYP8XYTI7vw9sQVnfB8f0J9GkYVgcWCIMfh9i0L6W+SOeOa9lxV08ZfSMjIvtJ9WgoKZzOha8LCA79EfsBMcJREBglDXzO0kKZVhhGJDUsiLtOaj1jxAwnXG6ADJdAVXRy4IzEGeCmgAcm7ld93ePiRLfzMFqbivtW0dJCluA3inoyagh95P+gudMiZG4ByOONwSdgljp7ikvG7UeL3xBYSHzPvJd/dMjBkC9+ox28khR0l8UrCjvQCnvFtyk9lh1+hItMyHnQL6qamQxOipCcJm2wrfxbkW4mddNJKRJzUJ9dzCVaGge0GB9dHgkwwiQ2T8tCQ2uLmPkbEsMx8xIB9RwyjK5THd4SyYd8YyqgrlKf3hLJWQNnuGWWzK5Sf7ghl27gxlK2mOd7eYz8yxz+TnI4fHxM8UUjyuzQrTAsdZ4XG/yIrLBAFgSuzQkuzchUZmt5p4mc3JVjpIkK9QJeElmqGltpZWvZAMNQnwczCfJPOP29edkDrzLIDar0uO5Kbupp+LdLCrEkL2CctLE17QAAYAFoGn8G1PJqGqj3Ymm1Di5+BSDWvjEk6OkMZQ1V7pYzWVeIzu6PEBxWXqn0nPsk02Grmc36KKc98Lk1lPUxMWgWWHaU+KDdlaHaeOEB7MDXD1C3T0A1gFaqvG4KQXVpN0oha2oWuIlCZ8PouEejzHUUgCAoJj9l3BCrTRK+JQPWT3OuS6RYjEKobgcANRyDrbHBoJwIZ2tkw994RqFrIFYGmxQikXYhAcXMVEYgHA5YfEvkIIodMNtxIE/a9ZcCLDmcw4faxCC2eg/2RPLH2XNevim0h3QWuiGTTtrIjKx+bgH4am2AJ34tfFbUXm6o13pYJoA8EEMMdFtLj3glQLf+2TAAwEEBkGfqtEaBMGX4XAsCBAALcwgLZUPsmQJly+y4EMAYCKBmF/1YIkFT8/gSwBgIop98AGyUSWbcEKFNCC97frvBGHDI89wvL0zKnbfnChclnMIXbHI4s9gLh/egzDvV9vNl6UWXxFSvPd7/gA92xpJmkVNQRXEysRamOgByLzBdtBWqUgwkh4wQmpHYpJCSw1MGJ3yfzsP83cRgOlnUgO4XEDenme7KCF4aNWIeScPbCXbiVtpLxxuhGnvTJIvnsnDJG17IQSm+llUauMsb8lztvoj4YisHvZsLL2rHMf8XlIZvQgEOPvQhIgrfslWxZXdTPDIGzOkQp1vDdsK7WBmsHZbVWUPZ4dNs3CcxNKBc9ao2PlGvMJsrRX/iRkLbiUZ0EzWih16BFl6yofryyZVaoAyPexIh9ng29EaQFQa8eQRoJevdLEK1kvd8tQ1pQ/OoxpJHid8cMsfpmSAuSYD2GNJIE75chKfS9MaQFzbAeQxpphvfLEFCiKXXLkBZExXoMaSQq3jFD+s5UQQuqYz2GoIEh1zCk7JupbhlS/YBmywwxB4ZcxZC+M1VQJoi+C0MafXNxvwwx+s5UQY132wfJvFXJ/JCHtDcFHXSmlcYtDAGiegDejoIOygTSAY4bka9BZ+Jkxc4yw3g9T5De5WvQmTg5HhhyFUN6XxR0Jk5e2oJmYMhtytegM3FyOjDkGob0Ll/DzsTJS+8GDwy5TfkadiZOPg4MuYYhvcvXsDNx8tLGSgNDblO+htXPeJ7A2IwynyvZUGN71ftlSO/yNYQnaIjXs59lUXow/4YCDdmKLmmA/S80cq1A5xdh7CCfx8c7RvPYHTeseDCUfjbrksHy2s26ar8I3gyOzva9vDTpf6QNG8zivpd9bxkDy1TIoo9r7WWmvmU0vX2LvRbHH6y7Z0yvu1bZ+b0UzPyGDQYAZWffumGDfX6jM7vXXatgZ+9rN3ps5sO8rGeifHDq/W1N2Nn72o2eivkwBLD1GyOAUaJNzQxlPFNGM2UGFZ47jDRlhhQ+jdoTZaYrVnSQJ4mTzuVHHvD53rZFSlykxpPHVru5qNOaKbalzGzFMhWbt2KJRkVzhmJZiq1X0UP2ItVD52EdomqwlKi8MXus2DNxMIKKNW3lJr9NHy/2nt8v9wAfGeJ+HxUbyb5w5wtXmMoIZHxiigPbjLCYKONRdPFjdGCKC5IE5uaGjY/nxB9j5/cyshcb566RSwkNynImNRxHP+0MPlTYLgWVDL50pDUcfbx4/Bcq8XR9/Ec0YPYf</diagram></mxfile>

docs/cs-basics/data-structure/pictures/树/顺序存储2.drawio

@@ -0,0 +1 @@
+<mxfile host="Electron" modified="2021-05-29T04:44:09.293Z" agent="5.0 (Macintosh; Intel Mac OS X 10_16_0) AppleWebKit/537.36 (KHTML, like Gecko) draw.io/13.4.5 Chrome/83.0.4103.122 Electron/9.1.0 Safari/537.36" etag="qoIVzM2KSH4_Q9T_5mZ7" version="13.4.5" type="device"><diagram id="KL8qVs7MDRylIb7IQKVJ" name="Page-1">7V1dc5s4FP01PDaDAPHxaDtOOp12p7PZ2W32ZUc2ss2WWC6WE3t//UogMGBhE4OBFqaZKbrCCO45ulwdybKiT172jwHarL4QF/uKprp7Rb9XNA0A1WT/ccshsjiOFRmWgeeKk46GJ+8/LIyqsO48F28zJ1JCfOptssY5Wa/xnGZsKAjIW/a0BfGzrW7QEp8YnubIP7X+5bl0FVltzTraP2JvuYpbBqYT1byg+GTxJNsVcslbyqRPFX0SEEKjo5f9BPvcebFfos89FNQmNxbgNS3zgd/G33/s9s92oH3Bn/w9/DH+MvsgrvKK/J14YEUzfXa98YzfMj0IP5g/dvw+xwuyph+2IUojdoIGN/tjJTta8v9H8TXYzcxio3BCckWN3R0DkRXGbyuP4qcNmvOaN8YjZlvRF5+VADtE202E7MLbY5ffhOf7E+KTILyQvlhgcz5n9i0NyHecqnEtZ6aqSeNpX8UPjgOK9ymT8N0jJi+YBgd2iqi1ocBREFmPcX1L0UKYVilGxDYkiLhMrnzEih0IuN4BnSaBLu/itTvifYCV1mSNs25lrggO39KF53Thnj+3mpQOolToyS3ZBXN85n510XtRsMT0MiWxm+mYp7ik/A4lfo9tAfYR9V6z3VkGhmjhK/HYkx1hj3u6gN3Uc3hGzy0+le5+uQs5AN5ptqFZQDMsw4zvRFzWUO1srZ5tJfLaSSshcRKfXM8lvTAMbDdofX0kSAWTyDCRh4bEFjX3a0QMoKrZkGG0HTKMpmAe9whmS+sYyrAplO97hLJpZFGGassom02h/NAjlIFqdwxmq2qWt/fot9Txc5zVseNjiscLcYaX5IVJ4bZ5ofFT5oVWjihJfHh3XmjYWcbFCDeU+tlVCSYdRqgX6BLTUk3REpyl5e0JBjtFMDv/wtGuJJht2ecGHlqrAw+nIvuuZ4VZkhV6p1jhGODO1HWoGzYjhAayYEIA7hzgsJDCagxTta4MSdA8wxgI1DYZEwuDt098HnuU+OQHMdBuOe8BMmWyauJz/g0jT3wuvcmuj0CwbOKjdioEWU7mjQGc7PuEBSgLQIu9dqAGdTt3+dIvLU16mbgRIL2FpiKQ1lQE+tijCHSilrUfgmSq6K8VguKofzkGaT9TDJLX1huDoLy2qRhULOXyUFNjDAIXYlDUXEEMYn2fZvtENoaIPpMOOMKEfG+5ZsU54zRm9jGPJN4c+SNR8eK5rl8U3QKyW7s8lp3vH++Y/QPZ4KTrp8HJkPA9P2irLzgVq7w1E0AbCMBqTCun8rdOgGIBuGYC6AMBFD4o7hoBZNLwTQhgDATgESCfn4K2CSCTbm9CAGcgACdAXvKXzA01SwDnxNk8P38SReHFrB9IQFdkSdbI/0zIRgDyL6b0INbeoR0lilzhV++g0siUULzQr64podKjjWoLshpTJqc90gWcvDLZ9oysVlmZvGqC9f0Tudf3v9KyQLcmRwDIjsmtrCwADV1W+15ZAKhnJ9QYP9ucHonJePukwBySAh5mnI5lhVrxWs6aCWANBAjDAewaA5rTBgdpIExRzI4NDDSZOJjz/naFNvyQopmfS1BkTtuy9xYVQwTutjlDFnlr7v3wM3Pi+2iz9cKLRWesPN/9jA5kR+Nm4lI+k3QRthfSTNKc23i2qAemRLERMFmSjuqojaaSMg2vACf26NRD/u8sJUfrZRnITiFxA7L5I87puGHD0xAcTF+ZV7fCJulvNBwp8kofL+LPzgil5EUUAuGt5KKhq+CY/THnTfjIEbKnmbAyOJbZHz89oBOyZtAjL8QWoy19w1sqRf083y9z4RLW+WV89WFdg1ynlorKHotu+yqBuQrlwm/hoSPlKrOJMFAXfjiUWrGojtfvoIV5DS3MRllRg4ZXjhXqwIh3MWKfZUNrBJGtkLwJQSpN9PaXIEDydZ9GGRJnNbdniDYw5CqGSBYyNcuQ4m9518yQSuPB/jIkgb41htSgGpZjSKW55P4yRJdICs0ypAZZsRxD4MCQqxjSdqaq1yA7lmNIpZmH/jJE9sX0ZhlSw5rFcgypNDXRY4a0nqnWsKixHEPsgSHXMAS2nqkWy6iz6+lRsMBtgD2/9rE12It10gqwgwJRdMA9xr31pLJY/qyCe4HWOeCe/zpwW7gbxaJmFdwLFMwB9/yuJq3hXnVDSjnuBbrkgHt+s5HWcJcJkDXCM6yEOIH+kIW0tYURRmPKYtTCMO479rbuLowwZGriAEdHViUYjSl5BXtJD/2146sSjMaUvPHAkKsY0nqq39iCyEubTg8M6eaqBKOxxZH3A0OuYUjrqxKMEvtH9hiettNEWKzilf5GdLkOXOkb0f1lSOtLAmCx3lczQyptY95jhrSdJsIbK4M/Nzytz8fDGn46plwHrrQdb38Z0vrUPTQGNLozoQ7hgEZ3prmhOaDRnclnWKxI1fwuq7Sxc38Z0uQ0NWtt/s/u9dMfSH3Wta+Pf/+528h+LnMKFTb6HE2VqaGwQcYIKFNTcVTFmShTTbHDg6xoNU+2NzjyRF8sHId/xyJPnUePrnYzfk17qji2MnUU21Ic1orNG+XNQcW2FUdTCuQqcReJxDULyhAZGFIis8acseJM+cHIUOz7Wh7y6/3Dxbtnz8s8MLbC531QHFPcC3M+d4WljPSUTyx+4FghFhNlPApPfggPLH5CHGo6tx2Jj2bYH6P592VozzfOXCM24QCGKKd2yxiH/5IeeNKxJBtoXI7G8aYmkswl2cGk4q4mrHj8HdxoJ6zjrwnr0/8B</diagram></mxfile>

docs/cs-basics/data-structure/图.md

@@ -11,7 +11,7 @@
 - 线性数据结构的元素满足唯一的线性关系，每个元素(除第一个和最后一个外)只有一个直接前趋和一个直接后继。
 - 树形数据结构的元素之间有着明显的层次关系。
 
-但是，树形结构的元素之间的关系是任意的。
+但是，图形结构的元素之间的关系是任意的。
 
 **何为图呢？** 简单来说，图就是由顶点的有穷非空集合和顶点之间的边组成的集合。通常表示为：**G(V,E)**，其中，G表示一个图，V表示顶点的集合，E表示边的集合。
 

docs/cs-basics/data-structure/堆.md

@@ -0,0 +1,192 @@
+# 堆
+
+## 什么是堆
+
+堆是一种满足以下条件的树：
+
+堆中的每一个节点值都大于等于（或小于等于）子树中所有节点的值。或者说，任意一个节点的值都大于等于（或小于等于）所有子节点的值。
+
+> 大家可以把堆(最大堆)理解为一个公司,这个公司很公平,谁能力强谁就当老大,不存在弱的人当老大,老大手底下的人一定不会比他强。这样有助于理解后续堆的操作。
+
+**!!!特别提示：**
+
+- 很多博客说堆是完全二叉树，其实并非如此，**堆不一定是完全二叉树**，只是为了方便存储和索引，我们通常用完全二叉树的形式来表示堆，事实上，广为人知的斐波那契堆和二项堆就不是完全二叉树,它们甚至都不是二叉树。
+- （**二叉**）堆是一个数组，它可以被看成是一个 **近似的完全二叉树**。——《算法导论》第三版
+
+大家可以尝试判断下面给出的图是否是二叉树？
+
+![](pictures/堆/堆1.png)
+
+第1个和第2个是堆。第1个是最大堆，每个节点都比子树中所有节点大。第2个是最小堆，每个节点都比子树中所有节点小。
+
+第3个不是，第三个中，根结点1比2和15小，而15却比3大，19比5大，不满足堆的性质。
+
+## 堆的用途
+当我们只关心所有数据中的最大值或者最小值，存在多次获取最大值或者最小值，多次插入或删除数据时，就可以使用堆。
+
+有小伙伴可能会想到用有序数组，初始化一个有序数组时间复杂度是 `O(nlog(n))`，查找最大值或者最小值时间复杂度都是 `O(1)`，但是，涉及到更新（插入或删除）数据时，时间复杂度为 `O(n)`，即使是使用复杂度为 `O(log(n))` 的二分法找到要插入或者删除的数据，在移动数据时也需要 `O(n)` 的时间复杂度。
+
+**相对于有序数组而言，堆的主要优势在于更新数据效率较高。** 堆的初始化时间复杂度为 `O(nlog(n))`，堆可以做到`O(1)`时间复杂度取出最大值或者最小值，`O(log(n))`时间复杂度插入或者删除数据，具体操作在后续章节详细介绍。
+
+## 堆的分类
+
+堆分为 **最大堆** 和 **最小堆**。二者的区别在于节点的排序方式。
+- **最大堆** ：堆中的每一个节点的值都大于等于子树中所有节点的值
+- **最小堆** ：堆中的每一个节点的值都小于等于子树中所有节点的值
+
+如下图所示，图1是最大堆，图2是最小堆
+
+![](pictures/堆/堆2.png)
+
+
+## 堆的存储
+之前介绍树的时候说过，由于完全二叉树的优秀性质，利用数组存储二叉树即节省空间，又方便索引（若根结点的序号为1，那么对于树中任意节点i，其左子节点序号为 `2\*i`，右子节点序号为 `2\*i+1`）。
+
+为了方便存储和索引，（二叉）堆可以用完全二叉树的形式进行存储。存储的方式如下图所示：
+
+![堆的存储](pictures/堆/堆的存储.png)
+
+## 堆的操作
+堆的更新操作主要包括两种 :  **插入元素** 和 **删除堆顶元素**。操作过程需要着重掌握和理解。
+> 在进入正题之前，再重申一遍，堆是一个公平的公司，有能力的人自然会走到与他能力所匹配的位置
+### 插入元素
+> 插入元素，作为一个新入职的员工，初来乍到，这个员工需要从基层做起
+
+**1.将要插入的元素放到最后**
+
+![堆-插入元素-1](pictures/堆/堆-插入元素1.png)
+
+> 有能力的人会逐渐升职加薪，是金子总会发光的！！！
+
+**2.从底向上，如果父结点比该元素大，则该节点和父结点交换，直到无法交换**
+
+![堆-插入元素2](pictures/堆/堆-插入元素2.png)
+
+![堆-插入元素3](pictures/堆/堆-插入元素3.png)
+
+### 删除堆顶元素
+
+根据堆的性质可知，最大堆的堆顶元素为所有元素中最大的，最小堆的堆顶元素是所有元素中最小的。当我们需要多次查找最大元素或者最小元素的时候，可以利用堆来实现。
+
+删除堆顶元素后，为了保持堆的性质，需要对堆的结构进行调整，我们将这个过程称之为"**堆化**"，堆化的方法分为两种：
+
+- 一种是自底向上的堆化，上述的插入元素所使用的就是自底向上的堆化，元素从最底部向上移动。
+- 另一种是自顶向下堆化，元素由最顶部向下移动。在讲解删除堆顶元素的方法时，我将阐述这两种操作的过程，大家可以体会一下二者的不同。
+
+#### 自底向上堆化
+
+> 在堆这个公司中，会出现老大离职的现象，老大离职之后，他的位置就空出来了
+
+首先删除堆顶元素，使得数组中下标为1的位置空出。
+
+
+
+![删除堆顶元素1](pictures/堆/删除堆顶元素1.png)
+
+
+> 那么他的位置由谁来接替呢，当然是他的直接下属了，谁能力强就让谁上呗
+
+比较根结点的左子节点和右子节点，也就是下标为2,3的数组元素，将较大的元素填充到根结点(下标为1)的位置。
+
+![删除堆顶元素2](pictures/堆/删除堆顶元素2.png)
+
+
+> 这个时候又空出一个位置了，老规矩，谁有能力谁上
+
+一直循环比较空出位置的左右子节点，并将较大者移至空位，直到堆的最底部
+
+![删除堆顶元素3](pictures/堆/删除堆顶元素3.png)
+
+这个时候已经完成了自底向上的堆化，没有元素可以填补空缺了，但是，我们可以看到数组中出现了“气泡”，这会导致存储空间的浪费。接下来我们试试自顶向下堆化。
+
+#### 自顶向下堆化
+自顶向下的堆化用一个词形容就是“石沉大海”，那么第一件事情，就是把石头抬起来，从海面扔下去。这个石头就是堆的最后一个元素，我们将最后一个元素移动到堆顶。
+
+![删除堆顶元素4](pictures/堆/删除堆顶元素4.png)
+
+然后开始将这个石头沉入海底，不停与左右子节点的值进行比较，和较大的子节点交换位置，直到无法交换位置。
+
+![删除堆顶元素5](pictures/堆/删除堆顶元素5.png)
+
+![删除堆顶元素6](pictures/堆/删除堆顶元素6.png)
+
+
+
+### 堆的操作总结
+
+- **插入元素** ：先将元素放至数组末尾，再自底向上堆化，将末尾元素上浮
+- **删除堆顶元素** ：删除堆顶元素，将末尾元素放至堆顶，再自顶向下堆化，将堆顶元素下沉。也可以自底向上堆化，只是会产生“气泡”，浪费存储空间。最好采用自顶向下堆化的方式。
+
+
+## 堆排序
+
+堆排序的过程分为两步：
+
+- 第一步是建堆，将一个无序的数组建立为一个堆
+- 第二步是排序，将堆顶元素取出，然后对剩下的元素进行堆化，反复迭代，直到所有元素被取出为止。
+
+### 建堆
+
+如果你已经足够了解堆化的过程，那么建堆的过程掌握起来就比较容易了。建堆的过程就是一个对所有非叶节点的自顶向下堆化过程。
+
+首先要了解哪些是非叶节点，最后一个节点的父结点及它之前的元素，都是非叶节点。也就是说，如果节点个数为n，那么我们需要对n/2到1的节点进行自顶向下（沉底）堆化。
+
+具体过程如下图：
+
+![建堆1](pictures/堆/建堆1.png)
+
+将初始的无序数组抽象为一棵树，图中的节点个数为6，所以4,5,6节点为叶节点，1,2,3节点为非叶节点，所以要对1-3号节点进行自顶向下（沉底）堆化，注意，顺序是从后往前堆化，从3号节点开始，一直到1号节点。
+3号节点堆化结果：
+
+![建堆1](pictures/堆/建堆2.png)
+
+2号节点堆化结果：
+
+![建堆1](pictures/堆/建堆3.png)
+
+1号节点堆化结果：
+
+![建堆1](pictures/堆/建堆4.png)
+
+至此，数组所对应的树已经成为了一个最大堆，建堆完成！
+
+### 排序
+
+由于堆顶元素是所有元素中最大的，所以我们重复取出堆顶元素，将这个最大的堆顶元素放至数组末尾，并对剩下的元素进行堆化即可。
+
+现在思考两个问题：
+
+- 删除堆顶元素后需要执行自顶向下（沉底）堆化还是自底向上（上浮）堆化？
+- 取出的堆顶元素存在哪，新建一个数组存？
+
+先回答第一个问题，我们需要执行自顶向下（沉底）堆化，这个堆化一开始要将末尾元素移动至堆顶，这个时候末尾的位置就空出来了，由于堆中元素已经减小，这个位置不会再被使用，所以我们可以将取出的元素放在末尾。
+
+机智的小伙伴已经发现了，这其实是做了一次交换操作，将堆顶和末尾元素调换位置，从而将取出堆顶元素和堆化的第一步(将末尾元素放至根结点位置)进行合并。
+
+详细过程如下图所示：
+
+取出第一个元素并堆化：
+
+![堆排序1](pictures/堆/堆排序1.png)
+
+取出第二个元素并堆化：
+
+![堆排序2](pictures/堆/堆排序2.png)
+
+取出第三个元素并堆化：
+
+![堆排序3](pictures/堆/堆排序3.png)
+
+取出第四个元素并堆化：
+
+![堆排序4](pictures/堆/堆排序4.png)
+
+取出第五个元素并堆化：
+
+![堆排序5](pictures/堆/堆排序5.png)
+
+取出第六个元素并堆化：
+
+![堆排序6](pictures/堆/堆排序6.png)
+
+堆排序完成！

docs/cs-basics/data-structure/树.md

@@ -0,0 +1,174 @@
+# 树
+
+树就是一种类似现实生活中的树的数据结构（倒置的树）。任何一颗非空树只有一个根节点。
+
+一棵树具有以下特点：
+
+1. 一棵树中的任意两个结点有且仅有唯一的一条路径连通。
+2. 一棵树如果有 n 个结点，那么它一定恰好有 n-1 条边。
+3. 一棵树不包含回路。
+
+下图就是一颗树，并且是一颗二叉树。
+
+![二叉树](https://my-blog-to-use.oss-cn-beijing.aliyuncs.com/2019-6/二叉树-2.png)
+
+如上图所示，通过上面这张图说明一下树中的常用概念：
+
+- **节点** ：树中的每个元素都可以统称为节点。
+- **根节点** ：顶层节点或者说没有父节点的节点。上图中 A 节点就是根节点。
+- **父节点** ：若一个节点含有子节点，则这个节点称为其子节点的父节点。上图中的 B 节点是 D 节点、E 节点的父节点。
+- **子节点** ：一个节点含有的子树的根节点称为该节点的子节点。上图中 D 节点、E 节点是 B 节点的子节点。
+- **兄弟节点** ：具有相同父节点的节点互称为兄弟节点。上图中 D 节点、E 节点的共同父节点是 B 节点，故 D 和 E 为兄弟节点。
+- **叶子节点** ：没有子节点的节点。上图中的 D、F、H、I 都是叶子节点。
+- **节点的高度** ：该节点到叶子节点的最长路径所包含的边数。
+- **节点的深度** ：根节点到该节点的路径所包含的边数
+- **节点的层数** ：节点的深度+1。
+- **树的高度** ：根节点的高度。
+
+## 二叉树的分类
+
+**二叉树**（Binary tree）是每个节点最多只有两个分支（即不存在分支度大于 2 的节点）的树结构。
+
+**二叉树** 的分支通常被称作“**左子树**”或“**右子树**”。并且，**二叉树** 的分支具有左右次序，不能随意颠倒。
+
+**二叉树** 的第 i 层至多拥有 `2^(i-1)` 个节点，深度为 k 的二叉树至多总共有 `2^k-1` 个节点
+
+### 满二叉树
+
+一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是 **满二叉树**。也就是说，如果一个二叉树的层数为 K，且结点总数是(2^k) -1 ，则它就是 **满二叉树**。如下图所示：
+
+![](./pictures/树/满二叉树.png)
+
+### 完全二叉树
+
+除最后一层外，若其余层都是满的，并且最后一层或者是满的，或者是在右边缺少连续若干节点，则这个二叉树就是 **完全二叉树** 。
+
+大家可以想象为一棵树从根结点开始扩展，扩展完左子节点才能开始扩展右子节点，每扩展完一层，才能继续扩展下一层。如下图所示：
+
+![](./pictures/树/完全二叉树.png)
+
+完全二叉树有一个很好的性质：**父结点和子节点的序号有着对应关系。**
+
+细心的小伙伴可能发现了，当根节点的值为 1 的情况下，若父结点的序号是 i，那么左子节点的序号就是 2i，右子节点的序号是 2i+1。这个性质使得完全二叉树利用数组存储时可以极大地节省空间，以及利用序号找到某个节点的父结点和子节点，后续二叉树的存储会详细介绍。
+
+### 平衡二叉树
+
+**平衡二叉树** 是一棵二叉排序树，且具有以下性质：
+
+1. 可以是一棵空树
+2. 如果不是空树，它的左右两个子树的高度差的绝对值不超过 1，并且左右两个子树都是一棵平衡二叉树。
+
+平衡二叉树的常用实现方法有 **红黑树**、**AVL 树**、**替罪羊树**、**加权平衡树**、**伸展树** 等。
+
+在给大家展示平衡二叉树之前，先给大家看一棵树：
+
+![](./pictures/树/斜树.png)
+
+**你管这玩意儿叫树？？？**
+
+没错，这玩意儿还真叫树，只不过这棵树已经退化为一个链表了，我们管它叫 **斜树**。
+
+**如果这样，那我为啥不直接用链表呢?**
+
+谁说不是呢？
+
+二叉树相比于链表，由于父子节点以及兄弟节点之间往往具有某种特殊的关系，这种关系使得我们在树中对数据进行**搜索**和**修改**时，相对于链表更加快捷便利。
+
+但是，如果二叉树退化为一个链表了，那么那么树所具有的优秀性质就难以表现出来，效率也会大打折，为了避免这样的情况，我们希望每个做 “家长”（父结点） 的，都 **一碗水端平**，分给左儿子和分给右儿子的尽可能一样多，相差最多不超过一层，如下图所示：
+
+![](./pictures/树/平衡二叉树.png)
+
+## 二叉树的存储
+
+二叉树的存储主要分为 **链式存储** 和 **顺序存储** 两种：
+
+### 链式存储
+
+和链表类似，二叉树的链式存储依靠指针将各个节点串联起来，不需要连续的存储空间。
+
+每个节点包括三个属性：
+
+- 数据 data。data 不一定是单一的数据，根据不同情况，可以是多个具有不同类型的数据。
+- 左节点指针 left
+- 右节点指针 right。
+
+可是 JAVA 没有指针啊！
+
+那就直接引用对象呗（别问我对象哪里找）
+
+![](./pictures/树/链式存储二叉树.png)
+
+### 顺序存储
+
+顺序存储就是利用数组进行存储，数组中的每一个位置仅存储节点的 data，不存储左右子节点的指针，子节点的索引通过数组下标完成。根结点的序号为 1，对于每个节点 Node，假设它存储在数组中下标为 i 的位置，那么它的左子节点就存储在 2 _ i 的位置，它的右子节点存储在下标为 2 _ i+1 的位置。
+
+一棵完全二叉树的数组顺序存储如下图所示：
+
+![](./pictures/树/顺序存储.png)
+
+大家可以试着填写一下存储如下二叉树的数组，比较一下和完全二叉树的顺序存储有何区别：
+
+![](./pictures/树/顺序存储2.png)
+
+可以看到，如果我们要存储的二叉树不是完全二叉树，在数组中就会出现空隙，导致内存利用率降低
+
+## 二叉树的遍历
+
+### 先序遍历
+
+![](./pictures/树/先序遍历.png)
+
+二叉树的先序遍历，就是先输出根结点，再遍历左子树，最后遍历右子树，遍历左子树和右子树的时候，同样遵循先序遍历的规则，也就是说，我们可以递归实现先序遍历。
+
+代码如下：
+
+```java
+public void preOrder(TreeNode root){
+	if(root == null){
+		return;
+	}
+	system.out.println(root.data);
+	preOrder(root.left);
+	preOrder(root.right);
+}
+```
+
+### 中序遍历
+
+![](./pictures/树/中序遍历.png)
+
+二叉树的中序遍历，就是先递归中序遍历左子树，再输出根结点的值，再递归中序遍历右子树，大家可以想象成一巴掌把树压扁，父结点被拍到了左子节点和右子节点的中间，如下图所示：
+
+![](./pictures/树/中序遍历2.png)
+
+代码如下：
+
+```java
+public void inOrder(TreeNode root){
+	if(root == null){
+		return;
+	}
+	inOrder(root.left);
+	system.out.println(root.data);
+	inOrder(root.right);
+}
+```
+
+### 后序遍历
+
+![](./pictures/树/后序遍历.png)
+
+二叉树的后序遍历，就是先递归后序遍历左子树，再递归后序遍历右子树，最后输出根结点的值
+
+代码如下：
+
+```java
+public void postOrder(TreeNode root){
+	if(root == null){
+		return;
+	}
+	postOrder(root.left);
+	postOrder(root.right);
+	system.out.println(root.data);
+}
+```