Merge pull request #2380 from zhangxqsgithub/main

给出 JVM 的英文全称

docs/cs-basics/algorithms/10-classical-sorting-algorithms.md

@@ -11,41 +11,37 @@ tag:
 
 所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。排序算法，就是如何使得记录按照要求排列的方法。排序算法在很多领域得到相当地重视，尤其是在大量数据的处理方面。一个优秀的算法可以节省大量的资源。在各个领域中考虑到数据的各种限制和规范，要得到一个符合实际的优秀算法，得经过大量的推理和分析。
 
-两年前，我曾在[博客园](https://www.cnblogs.com/guoyaohua/)发布过一篇[《十大经典排序算法最强总结（含 JAVA 代码实现）》](https://www.cnblogs.com/guoyaohua/p/8600214.html)博文，简要介绍了比较经典的十大排序算法，不过在之前的博文中，仅给出了 Java 版本的代码实现，并且有一些细节上的错误。所以，今天重新写一篇文章，深入了解下十大经典排序算法的原理及实现。
-
 ## 简介
 
-排序算法可以分为：
+### 排序算法总结
 
-- **内部排序**：数据记录在内存中进行排序。
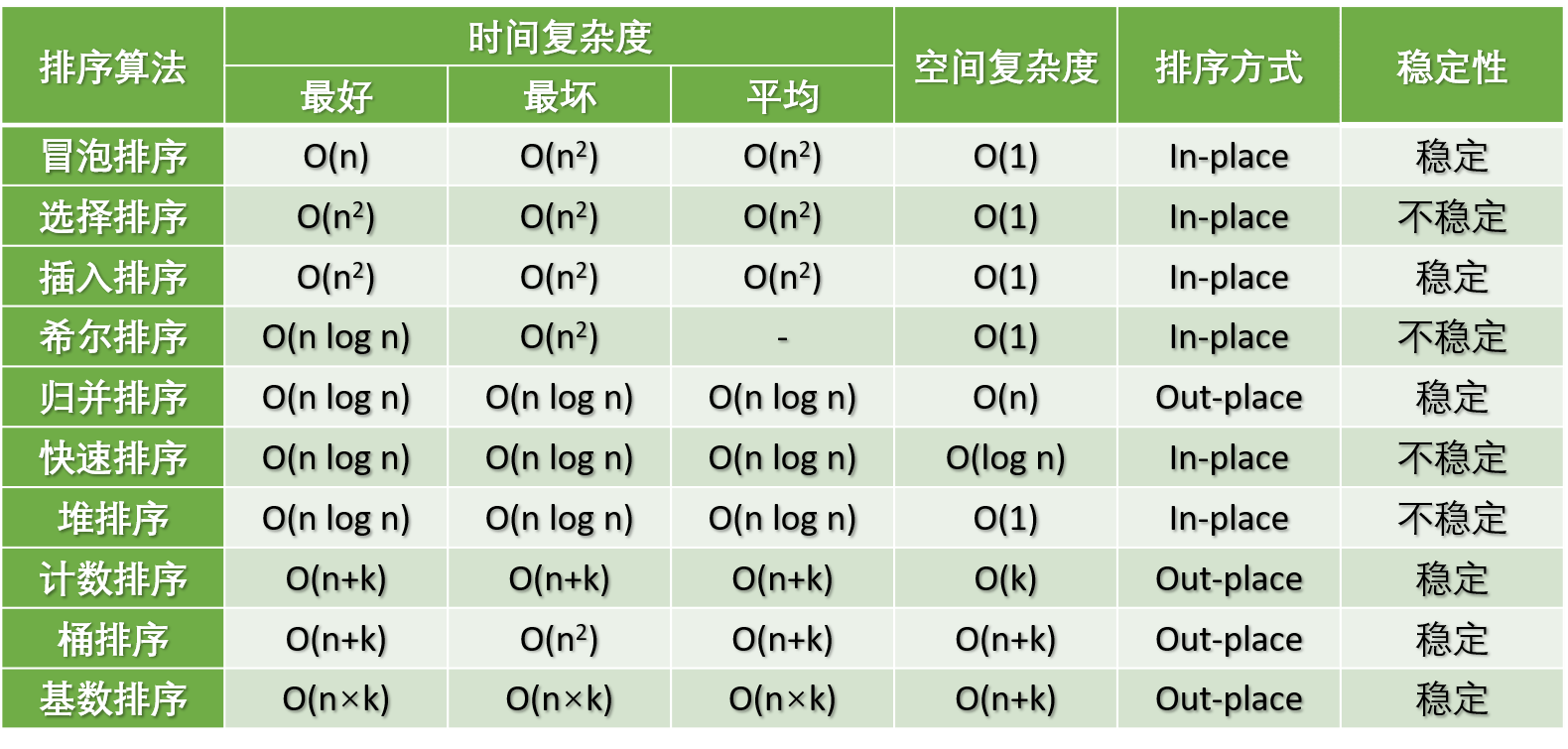
+常见的内部排序算法有：**插入排序**、**希尔排序**、**选择排序**、**冒泡排序**、**归并排序**、**快速排序**、**堆排序**、**基数排序**等，本文只讲解内部排序算法。用一张表格概括：
-- **[外部排序](https://zh.wikipedia.org/wiki/外排序)**：因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。
 
-常见的内部排序算法有：**插入排序**、**希尔排序**、**选择排序**、**冒泡排序**、**归并排序**、**快速排序**、**堆排序**、**基数排序**等，本文只讲解内部排序算法。用一张图概括：
+| 排序算法 | 时间复杂度（平均） | 时间复杂度（最差） | 时间复杂度（最好） | 空间复杂度 | 排序方式 | 稳定性 |
+| -------- | ------------------ | ------------------ | ------------------ | ---------- | -------- | ------ |
+| 冒泡排序 | O(n^2)             | O(n^2)             | O(n)               | O(1)       | 内部排序 | 稳定   |
+| 选择排序 | O(n^2)             | O(n^2)             | O(n^2)             | O(1)       | 内部排序 | 不稳定 |
+| 插入排序 | O(n^2)             | O(n^2)             | O(n)               | O(1)       | 内部排序 | 稳定   |
+| 希尔排序 | O(nlogn)           | O(n^2)             | O(nlogn)           | O(1)       | 内部排序 | 不稳定 |
+| 归并排序 | O(nlogn)           | O(nlogn)           | O(nlogn)           | O(n)       | 外部排序 | 稳定   |
+| 快速排序 | O(nlogn)           | O(n^2)             | O(nlogn)           | O(logn)    | 内部排序 | 不稳定 |
+| 堆排序   | O(nlogn)           | O(nlogn)           | O(nlogn)           | O(1)       | 内部排序 | 不稳定 |
+| 计数排序 | O(n+k)             | O(n+k)             | O(n+k)             | O(k)       | 外部排序 | 稳定   |
+| 桶排序   | O(n+k)             | O(n^2)             | O(n+k)             | O(n+k)     | 外部排序 | 稳定   |
+| 基数排序 | O(n×k)             | O(n×k)             | O(n×k)             | O(n+k)     | 外部排序 | 稳定   |
 
-![十大排序算法](https://oss.javaguide.cn/github/javaguide/cs-basics/sorting-algorithms/sort1.png)
+**术语解释**：
-
-上图存在错误：
-
-1. 插入排序的最好时间复杂度为 $O(n)$ 而不是 $O(n^2)$。
-2. 希尔排序的平均时间复杂度为 $O(nlogn)$。
-
-**图片名词解释：**
-
-- **n**：数据规模
-- **k**：“桶” 的个数
-- **In-place**：占用常数内存，不占用额外内存
-- **Out-place**：占用额外内存
-
-### 术语说明
 
+- **n**：数据规模，表示待排序的数据量大小。
+- **k**：“桶” 的个数，在某些特定的排序算法中（如基数排序、桶排序等），表示分割成的独立的排序区间或类别的数量。
+- **内部排序**：所有排序操作都在内存中完成，不需要额外的磁盘或其他存储设备的辅助。这适用于数据量小到足以完全加载到内存中的情况。
+- **外部排序**：当数据量过大，不可能全部加载到内存中时使用。外部排序通常涉及到数据的分区处理，部分数据被暂时存储在外部磁盘等存储设备上。
 - **稳定**：如果 A 原本在 B 前面，而 $A=B$，排序之后 A 仍然在 B 的前面。
 - **不稳定**：如果 A 原本在 B 的前面，而 $A=B$，排序之后 A 可能会出现在 B 的后面。
-- **内排序**：所有排序操作都在内存中完成。
-- **外排序**：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行。
 - **时间复杂度**：定性描述一个算法执行所耗费的时间。
 - **空间复杂度**：定性描述一个算法执行所需内存的大小。
 
-### 算法分类
+### 排序算法分类
 
 十种常见排序算法可以分类两大类别：**比较类排序**和**非比较类排序**。
 
@@ -401,7 +397,7 @@ public static void quickSort(int[] array, int low, int high) {
 ### 算法分析
 
 - **稳定性**：不稳定
-- **时间复杂度**：最佳：$O(nlogn)$， 最差：$O(nlogn)$，平均：$O(nlogn)$
+- **时间复杂度**：最佳：$O(nlogn)$， 最差：$O(n^2)$，平均：$O(nlogn)$
 - **空间复杂度**：$O(logn)$
 
 ## 堆排序 (Heap Sort)
@@ -565,13 +561,13 @@ public static int[] countingSort(int[] arr) {
 }
 ```
 
-## 算法分析
+### 算法分析
 
 当输入的元素是 `n` 个 `0` 到 `k` 之间的整数时，它的运行时间是 $O(n+k)$。计数排序不是比较排序，排序的速度快于任何比较排序算法。由于用来计数的数组 `C` 的长度取决于待排序数组中数据的范围（等于待排序数组的**最大值与最小值的差加上 1**），这使得计数排序对于数据范围很大的数组，需要大量额外内存空间。
 
 - **稳定性**：稳定
 - **时间复杂度**：最佳：$O(n+k)$ 最差：$O(n+k)$ 平均：$O(n+k)$
-- **空间复杂度**：`O(k)`
+- **空间复杂度**：$O(k)$
 
 ## 桶排序 (Bucket Sort)
 

docs/database/redis/redis-questions-02.md

@@ -665,6 +665,10 @@ Bloom Filter 会使用一个较大的 bit 数组来保存所有的数据，数
 
 根据用户或者 IP 对接口进行限流，对于异常频繁的访问行为，还可以采取黑名单机制，例如将异常 IP 列入黑名单。
 
+后面提到的缓存击穿和雪崩都可以配合接口限流来解决，毕竟这些问题的关键都是有很多请求落到了数据库上造成数据库压力过大。
+
+限流的具体方案可以参考这篇文章：[服务限流详解](https://javaguide.cn/high-availability/limit-request.html)。
+
 ### 缓存击穿
 
 #### 什么是缓存击穿？
@@ -677,9 +681,9 @@ Bloom Filter 会使用一个较大的 bit 数组来保存所有的数据，数
 
 #### 有哪些解决办法？
 
-1. 设置热点数据永不过期或者过期时间比较长。
+1. **永不过期**（不推荐）：设置热点数据永不过期或者过期时间比较长。
-2. 针对热点数据提前预热，将其存入缓存中并设置合理的过期时间比如秒杀场景下的数据在秒杀结束之前不过期。
+2. **提前预热**（推荐）：针对热点数据提前预热，将其存入缓存中并设置合理的过期时间比如秒杀场景下的数据在秒杀结束之前不过期。
-3. 请求数据库写数据到缓存之前，先获取互斥锁，保证只有一个请求会落到数据库上，减少数据库的压力。
+3. **加锁**（看情况）：在缓存失效后，通过设置互斥锁确保只有一个请求去查询数据库并更新缓存。
 
 #### 缓存穿透和缓存击穿有什么区别？
 
@@ -705,17 +709,16 @@ Bloom Filter 会使用一个较大的 bit 数组来保存所有的数据，数
 
 **针对 Redis 服务不可用的情况：**
 
-1. 采用 Redis 集群，避免单机出现问题整个缓存服务都没办法使用。
+1. **Redis 集群**：采用 Redis 集群，避免单机出现问题整个缓存服务都没办法使用。Redis Cluster 和 Redis Sentinel 是两种最常用的 Redis 集群实现方案，详细介绍可以参考：[Redis 集群详解(付费)](https://javaguide.cn/database/redis/redis-cluster.html)。
-2. 限流，避免同时处理大量的请求。
+2. **多级缓存**：设置多级缓存，例如本地缓存+Redis 缓存的二级缓存组合，当 Redis 缓存出现问题时，还可以从本地缓存中获取到部分数据。
-3. 多级缓存，例如本地缓存+Redis 缓存的组合，当 Redis 缓存出现问题时，还可以从本地缓存中获取到部分数据。
 
-**针对热点缓存失效的情况：**
+**针对大量缓存同时失效的情况：**
 
-1. 设置不同的失效时间比如随机设置缓存的失效时间。
+1. **设置随机失效时间**（可选）：为缓存设置随机的失效时间，例如在固定过期时间的基础上加上一个随机值，这样可以避免大量缓存同时到期，从而减少缓存雪崩的风险。
-2. 缓存永不失效（不太推荐，实用性太差）。
+2. **提前预热**（推荐）：针对热点数据提前预热，将其存入缓存中并设置合理的过期时间比如秒杀场景下的数据在秒杀结束之前不过期。
-3. 缓存预热，也就是在程序启动后或运行过程中，主动将热点数据加载到缓存中。
+3. **持久缓存策略**（看情况）：虽然一般不推荐设置缓存永不过期，但对于某些关键性和变化不频繁的数据，可以考虑这种策略。
 
-**缓存预热如何实现？**
+#### 缓存预热如何实现？
 
 常见的缓存预热方式有两种：
 

docs/java/basis/java-basic-questions-01.md

@@ -48,7 +48,7 @@ head:
 
 #### JVM
 
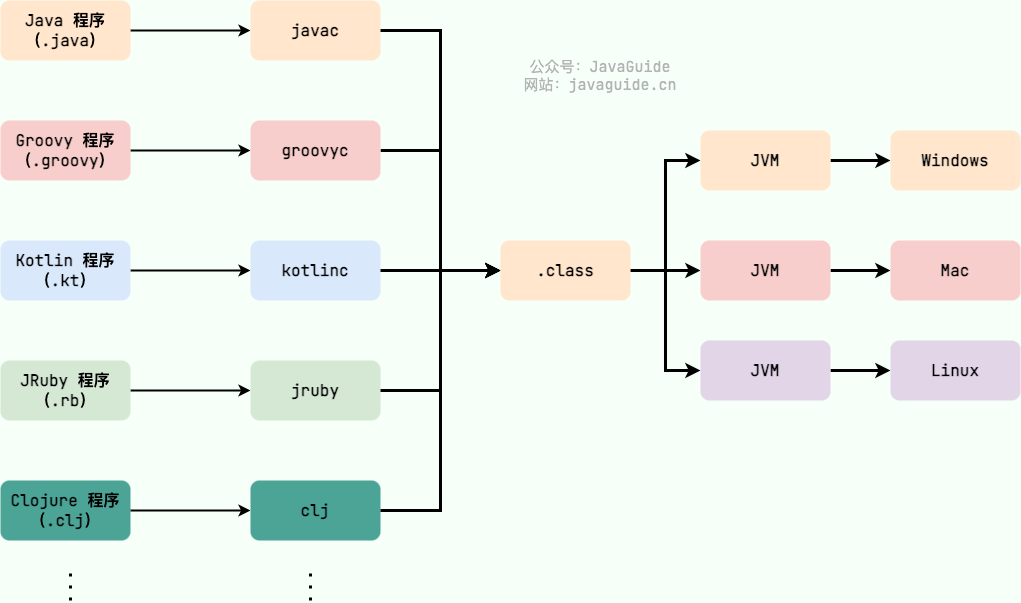
-Java 虚拟机（JVM）是运行 Java 字节码的虚拟机。JVM 有针对不同系统的特定实现（Windows，Linux，macOS），目的是使用相同的字节码，它们都会给出相同的结果。字节码和不同系统的 JVM 实现是 Java 语言“一次编译，随处可以运行”的关键所在。
+Java 虚拟机（Java Virtual Machine, JVM）是运行 Java 字节码的虚拟机。JVM 有针对不同系统的特定实现（Windows，Linux，macOS），目的是使用相同的字节码，它们都会给出相同的结果。字节码和不同系统的 JVM 实现是 Java 语言“一次编译，随处可以运行”的关键所在。
 
 ![运行在 Java 虚拟机之上的编程语言](https://oss.javaguide.cn/github/javaguide/java/basis/java-virtual-machine-program-language-os.png)
 

docs/java/basis/serialization.md

@@ -83,7 +83,7 @@ public class RpcRequest implements Serializable {
 
 ~~`static` 修饰的变量是静态变量，位于方法区，本身是不会被序列化的。 `static` 变量是属于类的而不是对象。你反序列之后，`static` 变量的值就像是默认赋予给了对象一样，看着就像是 `static` 变量被序列化，实际只是假象罢了。~~
 
-**🐛 修正（参见：[issue#2174](https://github.com/Snailclimb/JavaGuide/issues/2174)）**：`static` 修饰的变量是静态变量，位于方法区，本身是不会被序列化的。但是，`serialVersionUID` 的序列化做了特殊处理，在序列化时，会将 `serialVersionUID` 序列化到二进制字节流中；在反序列化时，也会解析它并做一致性判断。
+**🐛 修正（参见：[issue#2174](https://github.com/Snailclimb/JavaGuide/issues/2174)）**：`static` 修饰的变量是静态变量，属于类而非类的实例，本身是不会被序列化的。然而，`serialVersionUID` 是一个特例，`serialVersionUID` 的序列化做了特殊处理。当一个对象被序列化时，`serialVersionUID` 会被写入到序列化的二进制流中；在反序列化时，也会解析它并做一致性判断，以此来验证序列化对象的版本一致性。如果两者不匹配，反序列化过程将抛出 `InvalidClassException`，因为这通常意味着序列化的类的定义已经发生了更改，可能不再兼容。
 
 官方说明如下：
 

docs/java/jvm/jvm-garbage-collection.md

@@ -464,7 +464,7 @@ JDK1.8 默认使用的是 Parallel Scavenge + Parallel Old，如果指定了-XX:
 - **无法处理浮动垃圾；**
 - **它使用的回收算法-“标记-清除”算法会导致收集结束时会有大量空间碎片产生。**
 
-**CMS垃圾回收器在Java 9中已经被标记为过时(deprecated)，并在Java 14中被移除。**
+**CMS 垃圾回收器在 Java 9 中已经被标记为过时(deprecated)，并在 Java 14 中被移除。**
 
 ### G1 收集器