[docs update] 排序算法表格更新

docs/cs-basics/algorithms/10-classical-sorting-algorithms.md

@@ -11,41 +11,37 @@ tag:
 
 所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。排序算法，就是如何使得记录按照要求排列的方法。排序算法在很多领域得到相当地重视，尤其是在大量数据的处理方面。一个优秀的算法可以节省大量的资源。在各个领域中考虑到数据的各种限制和规范，要得到一个符合实际的优秀算法，得经过大量的推理和分析。
 
-两年前，我曾在[博客园](https://www.cnblogs.com/guoyaohua/)发布过一篇[《十大经典排序算法最强总结（含 JAVA 代码实现）》](https://www.cnblogs.com/guoyaohua/p/8600214.html)博文，简要介绍了比较经典的十大排序算法，不过在之前的博文中，仅给出了 Java 版本的代码实现，并且有一些细节上的错误。所以，今天重新写一篇文章，深入了解下十大经典排序算法的原理及实现。
-
 ## 简介
 
-排序算法可以分为：
+### 排序算法总结
 
-- **内部排序**：数据记录在内存中进行排序。
+常见的内部排序算法有：**插入排序**、**希尔排序**、**选择排序**、**冒泡排序**、**归并排序**、**快速排序**、**堆排序**、**基数排序**等，本文只讲解内部排序算法。用一张表格概括：
-- **[外部排序](https://zh.wikipedia.org/wiki/外排序)**：因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。
 
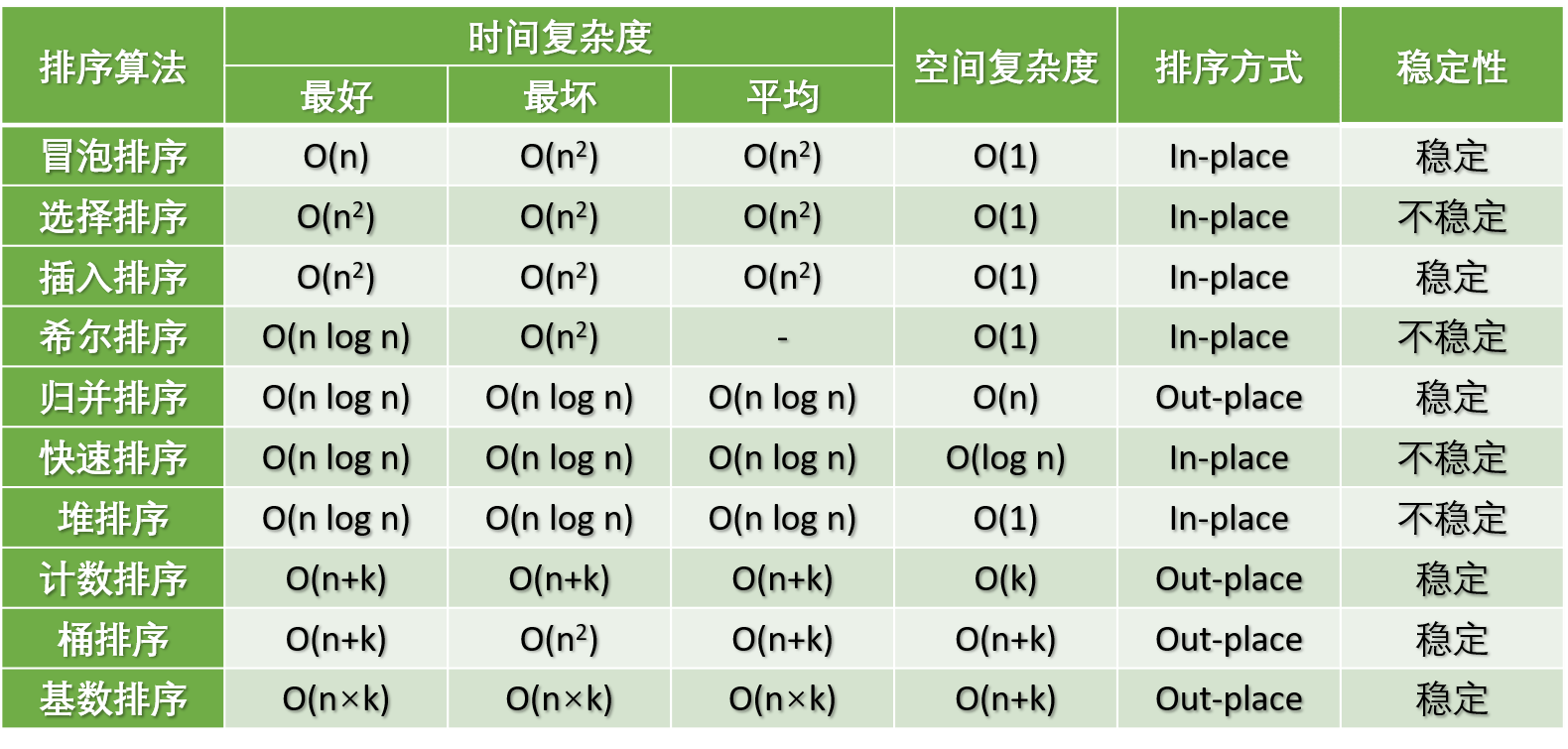
-常见的内部排序算法有：**插入排序**、**希尔排序**、**选择排序**、**冒泡排序**、**归并排序**、**快速排序**、**堆排序**、**基数排序**等，本文只讲解内部排序算法。用一张图概括：
+| 排序算法 | 时间复杂度（平均） | 时间复杂度（最差） | 时间复杂度（最好） | 空间复杂度 | 排序方式 | 稳定性 |
+| -------- | ------------------ | ------------------ | ------------------ | ---------- | -------- | ------ |
+| 冒泡排序 | O(n^2)             | O(n^2)             | O(n)               | O(1)       | 内部排序 | 稳定   |
+| 选择排序 | O(n^2)             | O(n^2)             | O(n^2)             | O(1)       | 内部排序 | 不稳定 |
+| 插入排序 | O(n)               | O(n^2)             | O(n^2)             | O(1)       | 内部排序 | 稳定   |
+| 希尔排序 | O(nlogn)           | O(n^2)             | O(nlogn)           | O(1)       | 内部排序 | 不稳定 |
+| 归并排序 | O(nlogn)           | O(nlogn)           | O(nlogn)           | O(n)       | 外部排序 | 稳定   |
+| 快速排序 | O(nlogn)           | O(n^2)             | O(nlogn)           | O(logn)    | 内部排序 | 不稳定 |
+| 堆排序   | O(nlogn)           | O(nlogn)           | O(nlogn)           | O(1)       | 内部排序 | 不稳定 |
+| 计数排序 | O(n+k)             | O(n+k)             | O(n+k)             | O(k)       | 外部排序 | 稳定   |
+| 桶排序   | O(n+k)             | O(n^2)             | O(n+k)             | O(n+k)     | 外部排序 | 稳定   |
+| 基数排序 | O(n×k)             | O(n×k)             | O(n×k)             | O(n+k)     | 外部排序 | 稳定   |
 
-![十大排序算法](https://oss.javaguide.cn/github/javaguide/cs-basics/sorting-algorithms/sort1.png)
+**术语解释**：
-
-上图存在错误：
-
-1. 插入排序的最好时间复杂度为 $O(n)$ 而不是 $O(n^2)$。
-2. 希尔排序的平均时间复杂度为 $O(nlogn)$。
-
-**图片名词解释：**
-
-- **n**：数据规模
-- **k**：“桶” 的个数
-- **In-place**：占用常数内存，不占用额外内存
-- **Out-place**：占用额外内存
-
-### 术语说明
 
+- **n**：数据规模，表示待排序的数据量大小。
+- **k**：“桶” 的个数，在某些特定的排序算法中（如基数排序、桶排序等），表示分割成的独立的排序区间或类别的数量。
+- **内部排序**：所有排序操作都在内存中完成，不需要额外的磁盘或其他存储设备的辅助。这适用于数据量小到足以完全加载到内存中的情况。
+- **外部排序**：当数据量过大，不可能全部加载到内存中时使用。外部排序通常涉及到数据的分区处理，部分数据被暂时存储在外部磁盘等存储设备上。
 - **稳定**：如果 A 原本在 B 前面，而 $A=B$，排序之后 A 仍然在 B 的前面。
 - **不稳定**：如果 A 原本在 B 的前面，而 $A=B$，排序之后 A 可能会出现在 B 的后面。
-- **内排序**：所有排序操作都在内存中完成。
-- **外排序**：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行。
 - **时间复杂度**：定性描述一个算法执行所耗费的时间。
 - **空间复杂度**：定性描述一个算法执行所需内存的大小。
 
-### 算法分类
+### 排序算法分类
 
 十种常见排序算法可以分类两大类别：**比较类排序**和**非比较类排序**。
 
@@ -401,7 +397,7 @@ public static void quickSort(int[] array, int low, int high) {
 ### 算法分析
 
 - **稳定性**：不稳定
-- **时间复杂度**：最佳：$O(nlogn)$， 最差：$O(nlogn)$，平均：$O(nlogn)$
+- **时间复杂度**：最佳：$O(nlogn)$， 最差：$O(n^2)$，平均：$O(nlogn)$
 - **空间复杂度**：$O(logn)$
 
 ## 堆排序 (Heap Sort)
@@ -565,13 +561,13 @@ public static int[] countingSort(int[] arr) {
 }
 ```
 
-## 算法分析
+### 算法分析
 
 当输入的元素是 `n` 个 `0` 到 `k` 之间的整数时，它的运行时间是 $O(n+k)$。计数排序不是比较排序，排序的速度快于任何比较排序算法。由于用来计数的数组 `C` 的长度取决于待排序数组中数据的范围（等于待排序数组的**最大值与最小值的差加上 1**），这使得计数排序对于数据范围很大的数组，需要大量额外内存空间。
 
 - **稳定性**：稳定
 - **时间复杂度**：最佳：$O(n+k)$ 最差：$O(n+k)$ 平均：$O(n+k)$
-- **空间复杂度**：`O(k)`
+- **空间复杂度**：$O(k)$
 
 ## 桶排序 (Bucket Sort)
 

docs/java/basis/serialization.md

@@ -83,7 +83,7 @@ public class RpcRequest implements Serializable {
 
 ~~`static` 修饰的变量是静态变量，位于方法区，本身是不会被序列化的。 `static` 变量是属于类的而不是对象。你反序列之后，`static` 变量的值就像是默认赋予给了对象一样，看着就像是 `static` 变量被序列化，实际只是假象罢了。~~
 
-**🐛 修正（参见：[issue#2174](https://github.com/Snailclimb/JavaGuide/issues/2174)）**：`static` 修饰的变量是静态变量，位于方法区，本身是不会被序列化的。但是，`serialVersionUID` 的序列化做了特殊处理，在序列化时，会将 `serialVersionUID` 序列化到二进制字节流中；在反序列化时，也会解析它并做一致性判断。
+**🐛 修正（参见：[issue#2174](https://github.com/Snailclimb/JavaGuide/issues/2174)）**：`static` 修饰的变量是静态变量，属于类而非类的实例，本身是不会被序列化的。然而，`serialVersionUID` 是一个特例，`serialVersionUID` 的序列化做了特殊处理。当一个对象被序列化时，`serialVersionUID` 会被写入到序列化的二进制流中；在反序列化时，也会解析它并做一致性判断，以此来验证序列化对象的版本一致性。如果两者不匹配，反序列化过程将抛出 `InvalidClassException`，因为这通常意味着序列化的类的定义已经发生了更改，可能不再兼容。
 
 官方说明如下：