[docs fix&update]修正网络部分的小错误+完善索引底层数据结构选型

docs/cs-basics/network/nat.md

@@ -7,7 +7,7 @@ tag:
 
 ## 应用场景
 
-**NAT 协议（Network Address Translation）** 的应用场景如同它的名称——网络地址转换，应用于内部网到外部网的地址转换过程中。具体地说，在一个小的子网（局域网，LAN）内，各主机使用的是同一个 LAN 下的 IP 地址，但在该 LAN 以外，在广域网（WAN）中，需要一个统一的 IP 地址来标识该 LAN 在整个 Internet 上的位置。
+**NAT 协议（Network Address Translation）** 的应用场景如同它的名称——网络地址转换，应用于内部网到外部网的地址转换过程中。具体地说，在一个小的子网（局域网，Local Area Network，LAN）内，各主机使用的是同一个 LAN 下的 IP 地址，但在该 LAN 以外，在广域网（Wide Area Network，WAN）中，需要一个统一的 IP 地址来标识该 LAN 在整个 Internet 上的位置。
 
 这个场景其实不难理解。随着一个个小型办公室、家庭办公室（Small Office, Home Office, SOHO）的出现，为了管理这些 SOHO，一个个子网被设计出来，从而在整个 Internet 中的主机数量将非常庞大。如果每个主机都有一个“绝对唯一”的 IP 地址，那么 IPv4 地址的表达能力可能很快达到上限（$2^{32}$）。因此，实际上，SOHO 子网中的 IP 地址是“相对的”，这在一定程度上也缓解了 IPv4 地址的分配压力。
 
@@ -17,7 +17,7 @@ SOHO 子网的“代理人”，也就是和外界的窗口，通常由路由器
 
 ![NAT 协议](https://oss.javaguide.cn/github/javaguide/cs-basics/network/nat-demo.png)
 
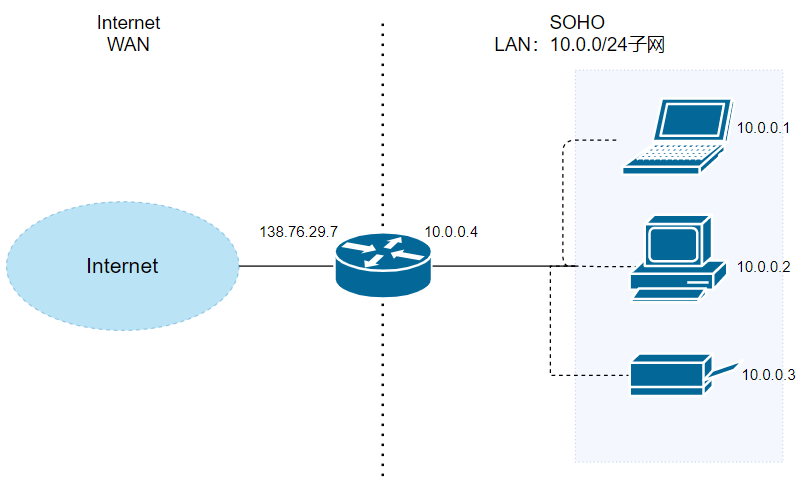
-假设当前场景如上图。中间是一个路由器，它的右侧组织了一个 WAN，该局域网的网络号为`10.0.0/24`，WAN 侧接口的 IP 地址为`10.0.0.4`，并且该子网内有至少三台主机，分别是`10.0.0.1`，`10.0.0.2`和`10.0.0.3`。路由器的左侧连接的是 WAN，WAN 侧接口的 IP 地址为`138.76.29.7`。
+假设当前场景如上图。中间是一个路由器，它的右侧组织了一个 LAN，网络号为`10.0.0/24`。LAN 侧接口的 IP 地址为`10.0.0.4`，并且该子网内有至少三台主机，分别是`10.0.0.1`，`10.0.0.2`和`10.0.0.3`。路由器的左侧连接的是 WAN，WAN 侧接口的 IP 地址为`138.76.29.7`。
 
 首先，针对以上信息，我们有如下事实需要说明：
 
@@ -38,6 +38,8 @@ SOHO 子网的“代理人”，也就是和外界的窗口，通常由路由器
 
 ![LAN-WAN 间通信提供地址转换](https://oss.javaguide.cn/github/javaguide/cs-basics/network/nat-demo2.png)
 
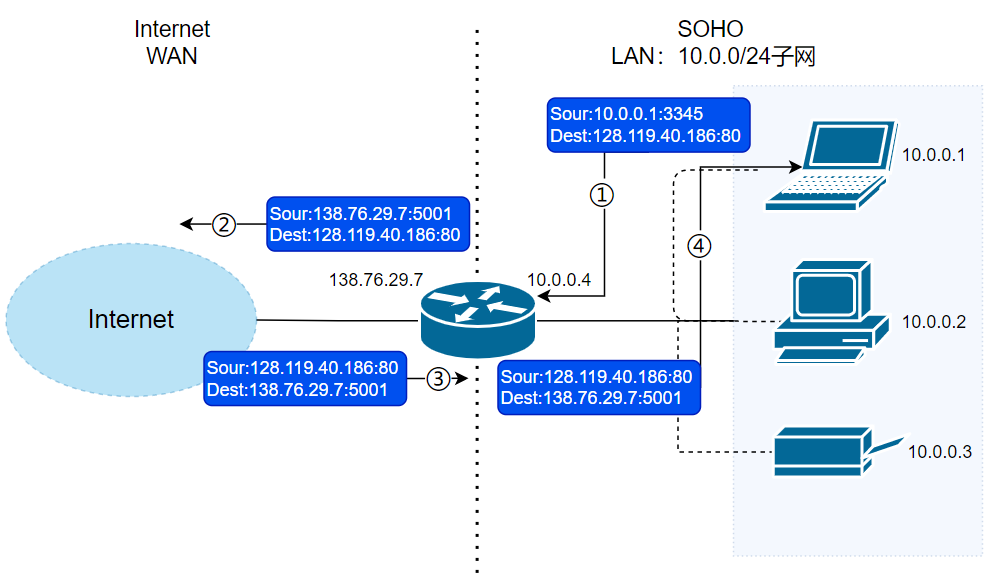
+🐛 修正（参见：[issue#2009](https://github.com/Snailclimb/JavaGuide/issues/2009)）：上图第四步的 Dest 值应该为 `10.0.0.1:3345` 而不是~~`138.76.29.7:5001`~~，这里笔误了。
+
 ## 划重点
 
 针对以上过程，有以下几个重点需要强调：

docs/database/mysql/mysql-index.md

@@ -35,7 +35,7 @@ tag:
 
 大多数情况下，索引查询都是比全表扫描要快的。但是如果数据库的数据量不大，那么使用索引也不一定能够带来很大提升。
 
-## 索引的底层数据结构
+## 索引底层数据结构选型
 
 ### Hash 表
 
@@ -66,6 +66,50 @@ SELECT * FROM tb1 WHERE id < 500;
 
 在这种范围查询中，优势非常大，直接遍历比 500 小的叶子节点就够了。而 Hash 索引是根据 hash 算法来定位的，难不成还要把 1 - 499 的数据，每个都进行一次 hash 计算来定位吗?这就是 Hash 最大的缺点了。
 
+### 二叉查找树(BST)
+
+二叉查找树（Binary Search Tree）是一种基于二叉树的数据结构，它具有以下特点：
+
+1. 左子树所有节点的值均小于根节点的值。
+2. 右子树所有节点的值均大于根节点的值。
+3. 左右子树也分别为二叉查找树。
+
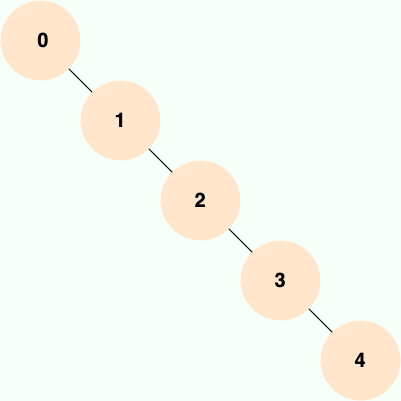
+当二叉查找树是平衡的时候，也就是树的每个节点的左右子树深度相差不超过 1 的时候，查询的时间复杂度为 O(log2(N))，具有比较高的效率。然而，当二叉查找树不平衡时，例如在最坏情况下（有序插入节点），树会退化成线性链表（也被称为斜树），导致查询效率急剧下降，时间复杂退化为 O（N）。
+
+![斜树](https://oss.javaguide.cn/github/javaguide/cs-basics/data-structure/oblique-tree.png)
+
+也就是说，**二叉查找树的性能非常依赖于它的平衡程度，这就导致其不适合作为 MySQL 底层索引的数据结构。**
+
+为了解决这个问题，并提高查询效率，人们发明了多种在二叉查找树基础上的改进型数据结构，如平衡二叉树、B-Tree、B+Tree 等。
+
+### AVL 树
+
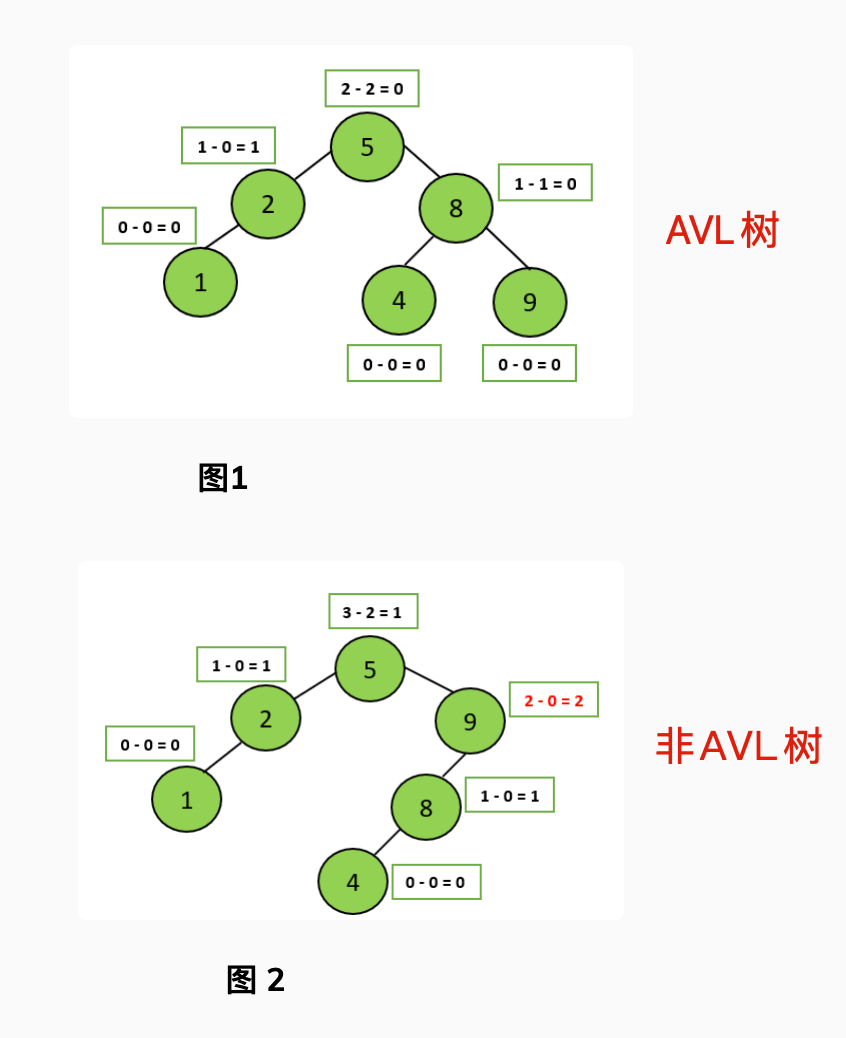
+AVL 树是计算机科学中最早被发明的自平衡二叉查找树，它的名称来自于发明者 G.M. Adelson-Velsky 和 E.M. Landis 的名字缩写。AVL 树的特点是保证任何节点的左右子树高度之差不超过 1，因此也被称为高度平衡二叉树，它的查找、插入和删除在平均和最坏情况下的时间复杂度都是 O(logn)。
+
+![AVL 树](https://oss.javaguide.cn/github/javaguide/cs-basics/data-structure/avl-tree.png)
+
+AVL 树采用了旋转操作来保持平衡。主要有四种旋转操作：LL 旋转、RR 旋转、LR 旋转和 RL 旋转。其中 LL 旋转和 RR 旋转分别用于处理左左和右右失衡，而 LR 旋转和 RL 旋转则用于处理左右和右左失衡。
+
+由于 AVL 树需要频繁地进行旋转操作来保持平衡，因此会有较大的计算开销进而降低了查询性能。并且， 在使用 AVL 树时，每个树节点仅存储一个数据，而每次进行磁盘 IO 时只能读取一个节点的数据，如果需要查询的数据分布在多个节点上，那么就需要进行多次磁盘 IO。 **磁盘 IO 是一项耗时的操作，在设计数据库索引时，我们需要优先考虑如何最大限度地减少磁盘 IO 操作的次数。**
+
+实际应用中，AVL 树使用的并不多。
+
+### 红黑树
+
+红黑树是一种自平衡二叉查找树，通过在插入和删除节点时进行颜色变换和旋转操作，使得树始终保持平衡状态，它具有以下特点：
+
+1. 每个节点非红即黑；
+2. 根节点总是黑色的；
+3. 每个叶子节点都是黑色的空节点（NIL 节点）；
+4. 如果节点是红色的，则它的子节点必须是黑色的（反之不一定）；
+5. 从根节点到叶节点或空子节点的每条路径，必须包含相同数目的黑色节点（即相同的黑色高度）。
+
+![红黑树](https://oss.javaguide.cn/github/javaguide/cs-basics/data-structure/red-black-tree.png)
+
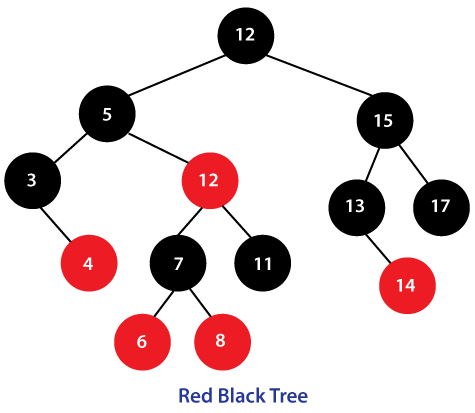
+和 AVL 树不同的是，红黑树并不追求严格的平衡，而是大致的平衡。正因如此，红黑树的查询效率稍有下降，因为红黑树的平衡性相对较弱，可能会导致树的高度较高，这可能会导致一些数据需要进行多次磁盘 IO 操作才能查询到，这也是 MySQL 没有选择红黑树的主要原因。也正因如此，红黑树的插入和删除操作效率大大提高了，因为红黑树在插入和删除节点时只需进行 O(1) 次数的旋转和变色操作，即可保持基本平衡状态，而不需要像 AVL 树一样进行 O(logn) 次数的旋转操作。
+
+**红黑树的应用还是比较广泛的，TreeMap、TreeSet 以及 JDK1.8 的 HashMap 底层都用到了红黑树。对于数据在内存中的这种情况来说，红黑树的表现是非常优异的。**
+
 ### B 树& B+树
 
 B 树也称 B-树,全称为 **多路平衡查找树** ，B+ 树是 B 树的一种变体。B 树和 B+树中的 B 是 `Balanced` （平衡）的意思。
@@ -77,6 +121,9 @@ B 树也称 B-树,全称为 **多路平衡查找树** ，B+ 树是 B 树的一
 - B 树的所有节点既存放键(key) 也存放数据(data)，而 B+树只有叶子节点存放 key 和 data，其他内节点只存放 key。
 - B 树的叶子节点都是独立的;B+树的叶子节点有一条引用链指向与它相邻的叶子节点。
 - B 树的检索的过程相当于对范围内的每个节点的关键字做二分查找，可能还没有到达叶子节点，检索就结束了。而 B+树的检索效率就很稳定了，任何查找都是从根节点到叶子节点的过程，叶子节点的顺序检索很明显。
+- 在 B 树中进行范围查询时，首先找到要查找的下限，然后对 B 树进行中序遍历，直到找到查找的上限；而 B+树的范围查询，只需要对链表进行遍历即可。
+
+综上，B+树与 B 树相比，具备更少的 IO 次数、更稳定的查询效率和更适于范围查询这些优势。
 
 在 MySQL 中，MyISAM 引擎和 InnoDB 引擎都是使用 B+Tree 作为索引结构，但是，两者的实现方式不太一样。（下面的内容整理自《Java 工程师修炼之道》）
 

docs/database/sql/sql-questions-01.md

@@ -564,7 +564,7 @@ FROM Customers
 
 知识点：
 
-- 截取函数`SUBSTRING()`：截取字符串，`substring(str ,n ,m)`：返回字符串 str 从第 n 个字符截取到第 m 个字符（左闭右闭）；
+- 截取函数`SUBSTRING()`：截取字符串，`substring(str ,n ,m)`（n 表示起始截取位置，m 表示要截取的字符个数）表示返回字符串 str 从第 n 个字符开始截取 m 个字符；
 - 拼接函数`CONCAT()`：将两个或多个字符串连接成一个字符串，select concat(A,B)：连接字符串 A 和 B。
 
 - 大写函数 `UPPER()`：将指定字符串转换为大写。

docs/database/sql/sql-syntax-summary.md

@@ -547,7 +547,7 @@ SELECT column_name(s) FROM table2;
 
 ## 函数
 
-不同数据库的函数往往各不相同，因此不可移植。本节主要以 MysSQL 的函数为例。
+不同数据库的函数往往各不相同，因此不可移植。本节主要以 MySQL 的函数为例。
 
 ### 文本处理
 

docs/java/concurrent/java-concurrent-questions-01.md

@@ -127,6 +127,13 @@ public class MultiThread {
 
 并发编程的目的就是为了能提高程序的执行效率提高程序运行速度，但是并发编程并不总是能提高程序运行速度的，而且并发编程可能会遇到很多问题，比如：内存泄漏、死锁、线程不安全等等。
 
+## 如何理解线程安全和不安全？
+
+线程安全和不安全是在多线程环境下对于同一份数据的访问是否能够保证其正确性和一致性的描述。
+
+- 线程安全指的是在多线程环境下，对于同一份数据，不管有多少个线程同时访问，都能保证这份数据的正确性和一致性。 
+- 线程不安全则表示在多线程环境下，对于同一份数据，多个线程同时访问时可能会导致数据混乱、错误或者丢失。
+
 ## 说说线程的生命周期和状态?
 
 Java 线程在运行的生命周期中的指定时刻只可能处于下面 6 种不同状态的其中一个状态：