[docs update]修正内容格式

docs/database/basis.md

@@ -65,7 +65,7 @@ ER 图由下面 3 个要素组成：
 - **函数依赖（functional dependency）**：若在一张表中，在属性（或属性组）X 的值确定的情况下，必定能确定属性 Y 的值，那么就可以说 Y 函数依赖于 X，写作 X → Y。
 - **部分函数依赖（partial functional dependency）**：如果 X→Y，并且存在 X 的一个真子集 X0，使得 X0→Y，则称 Y 对 X 部分函数依赖。比如学生基本信息表 R 中（学号，身份证号，姓名）当然学号属性取值是唯一的，在 R 关系中，（学号，身份证号）->（姓名），（学号）->（姓名），（身份证号）->（姓名）；所以姓名部分函数依赖于（学号，身份证号）；
 - **完全函数依赖(Full functional dependency)**：在一个关系中，若某个非主属性数据项依赖于全部关键字称之为完全函数依赖。比如学生基本信息表 R（学号，班级，姓名）假设不同的班级学号有相同的，班级内学号不能相同，在 R 关系中，（学号，班级）->（姓名），但是（学号）->(姓名)不成立，（班级）->(姓名)不成立，所以姓名完全函数依赖与（学号，班级）；
-- **传递函数依赖**：在关系模式 R(U)中，设 X，Y，Z 是 U 的不同的属性子集，如果 X 确定 Y、Y 确定 Z，且有 X 不包含 Y，Y 不确定 X，（X∪Y）∩Z=空集合，则称 Z 传递函数依赖(transitive functional dependency) 于 X。传递函数依赖会导致数据冗余和异常。传递函数依赖的 Y 和 Z 子集往往同属于某一个事物，因此可将其合并放到一个表中。比如在关系 R(学号 , 姓名, 系名，系主任)中，学号 → 系名，系名 → 系主任，所以存在非主属性系主任对于学号的传递函数依赖。。
+- **传递函数依赖**：在关系模式 R(U)中，设 X，Y，Z 是 U 的不同的属性子集，如果 X 确定 Y、Y 确定 Z，且有 X 不包含 Y，Y 不确定 X，（X∪Y）∩Z=空集合，则称 Z 传递函数依赖(transitive functional dependency) 于 X。传递函数依赖会导致数据冗余和异常。传递函数依赖的 Y 和 Z 子集往往同属于某一个事物，因此可将其合并放到一个表中。比如在关系 R(学号 , 姓名, 系名，系主任)中，学号 → 系名，系名 → 系主任，所以存在非主属性系主任对于学号的传递函数依赖。
 
 ### 3NF(第三范式)
 

docs/java/collection/java-collection-questions-02.md

@@ -79,20 +79,15 @@ head:
 ![TreeMap 继承关系图](https://oss.javaguide.cn/github/javaguide/java/collection/treemap_hierarchy.png)
 
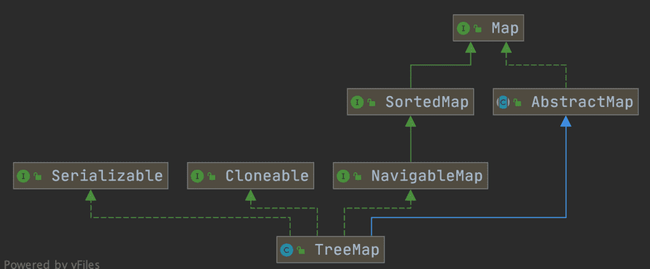
 实现 `NavigableMap` 接口让 `TreeMap` 有了对集合内元素的搜索的能力。
-```
+
-实现 NavigableMap 接口让 TreeMap 具备元素搜索能力
+`NavigableMap` 接口提供了丰富的方法来探索和操作键值对:
-`TreeMap` 是一种基于红黑树的 NavigableMap 实现，它存储的元素是有序的。实现 `NavigableMap` 接口使 `TreeMap` 具备了对集合内元素的高效搜索能力，提供了丰富的方法来探索和操作键值对。
+
-以下是实现 `NavigableMap` 接口为 `TreeMap` 带来的几个搜索相关的能力：
+1. **定向搜索**: `ceilingEntry()`, `floorEntry()`, `higherEntry()`和 `lowerEntry()` 等方法可以用于定位大于、小于、大于等于、小于等于给定键的最接近的键值对。
-1. **定向搜索**:
+2. **子集操作**: `subMap()`, `headMap()`和 `tailMap()` 方法可以高效地创建原集合的子集视图，而无需复制整个集合。
-   - `NavigableMap` 接口提供了 `ceilingEntry()`, `floorEntry()`, `higherEntry()`, 和 `lowerEntry()` 等方法，可以用于定位大于、小于、大于等于、小于等于给定键的最接近的键值对。
+3. **逆序视图**:`descendingMap()` 方法返回一个逆序的 `NavigableMap` 视图，使得可以反向迭代整个 `TreeMap`。
-2. **子集操作**:
+4. **边界操作**: `firstEntry()`, `lastEntry()`, `pollFirstEntry()`和 `pollLastEntry()` 等方法可以方便地访问和移除元素。
-   - 可以通过 `subMap()`, `headMap()`, 和 `tailMap()` 方法高效地创建原集合的子集视图，而无需复制整个集合。
+
-3. **逆序视图**:
-   - `descendingMap()` 方法返回一个逆序的 `NavigableMap` 视图，使得可以反向迭代整个 `TreeMap`。
-4. **边界操作**:
-   - 提供了 `firstEntry()`, `lastEntry()`, `pollFirstEntry()`, 和 `pollLastEntry()` 等方法来方便地访问和移除元素。
 这些方法都是基于红黑树数据结构的属性实现的，红黑树保持平衡状态，从而保证了搜索操作的时间复杂度为 O(log n)，这让 `TreeMap` 成为了处理有序集合搜索问题的强大工具。
-```
 
 实现`SortedMap`接口让 `TreeMap` 有了对集合中的元素根据键排序的能力。默认是按 key 的升序排序，不过我们也可以指定排序的比较器。示例代码如下：
 
@@ -152,7 +147,7 @@ TreeMap<Person, String> treeMap = new TreeMap<>((person1, person2) -> {
 });
 ```
 
-**综上，相比于`HashMap`来说 `TreeMap` 主要多了对集合中的元素根据键排序的能力以及对集合内元素的搜索的能力。**
+**综上，相比于`HashMap`来说， `TreeMap` 主要多了对集合中的元素根据键排序的能力以及对集合内元素的搜索的能力。**
 
 ### HashSet 如何检查重复?